1. 머신러닝이란?
- 머신러닝은 무엇을 의미하는가
강의에서 설명한 머신러닝을 정의하는 2가지 개념
(1) Arthur Samuel(1959) - 컴퓨터가 explicit하게 프로그램되지 않고 학습하도록 만드는 학문
(2) Tom Mitchell(1998) - 컴퓨터 프로그램이 경험 E로부터 어떤 task T를 하도록 배워서 T를 하는 성능 P가 좋아지는 과정을 컴퓨터가 'learn' 한다고 표현한다.
강의에서는 (1)은 조금 old하다고 표현했지만, 개인적으로는 (1)이 머신러닝이 필요한 이유라고 더 와닿았다.
수많은 데이터를 처리할 때 일일히 if문 등으로 처리하는 것(explicitly programmed)은 한계가 있기 때문에 머신러닝이 필요한 것이라고 생각한다.
- 머신러닝의 대표적인 종류
supervised learning과 unsupervised learning 2가지 종류가 대표적이며, 그 외에 reinforce learning등도 존재한다.
(1) supervised learning
모델을 학습시킬 때 right answer을 제공하여 학습시키는 방식.
다시 supervised learning은 regression과 classification 2가지 종류로 나눌 수 있다.
*regression?
: 연속적인 값을 예측하는 것.
ex) 실제 거래되었던 집값(right answer)을 보고 학습한 후,
새로운 집이 주어졌을 때 그 특징을 보고 집값을 예측하기.
*classification?
: 분류하는 것.
ex) 종양의 상태를 보고 악성인지 양성인지 판단하는 모델.
(2개 이상의 클래스로 분류할 수도 있다)
(2) unsupervised learning
모델 학습에 사용되는 데이터가 labeled 되어 있지 않은 상태로 학습하는 것.
모델이 데이터에서 structure를 찾고, 그에 따라 데이터를 분류함.
ex) 뉴스 기사들을 비슷한 카테고리끼리 묶음, Cockatil party problem
* Cocktail party problem : 칵테일 파티와 같이 다양한 음성, 소리가 뒤섞인 장소에서 하나의 음성만을 추출해내는 문제.
2. Model and Cost Function
- Univariate Linear Regression
$ h{_\Theta}(x) = \Theta{_0} + \Theta{_1}x $
단변수 선형 회귀 모델, 한가지의 feature 만으로 이루어진 선형회귀 모델.
$ \Theta $를 parameter라고 함.
- Cost Function
선형회귀 모델에서 cost fuction J는 다음과 같음.
$ J = \frac{1}{2m}\sum_{i=1}^{m}(h{_\Theta }(x{_i}) - y{_i})^{2} $
(m : 데이터 셋의 수, h : hypothesis)
식에서 확인할 수 있듯이 예측값과 실제값의 차의 제곱을 합하는 것이므로 squared error function이라고도 함.
직관적으로 위 데이터를 잘 설명할 수록 위 값이 작아질 것이라는 것을 알 수 있음.
*2로 나눈 이유는 gradient dicsent 를 적용할 때 미분 후 식을 간단하게 하기 위해서. 수식에 의미에는 영향 x
-> 주어진 데이터를 가장 잘 설명하는 모델을 찾는 것 = cost function을 최소화 하는 모델을 찾는 것
(물론 cost function을 다르게 정의할 수도 있지만 선형 회귀 모델에서는 위와 같이 정의함)
- Gradient Discent
Gradient Discent는 local minimum을 찾는 알고리즘으로, 일반적인 최적화 알고리즘이다.
선형 회귀 모델의 최적 파라미터($ \Theta $)를 계산하는 방법으로 적용가능(다른 방법도 존재)
-> 선형 회귀 모델의 cost function은 convex하다. 따라서 global minimum만 존재하고, gradient discent 기법으로 최적 파라미터를 찾을 수 있다.
univariate 모델에서 알고리즘 적용법 :
$ \Theta{_j} := \Theta{_j} - \alpha \frac{\partial }{\partial \Theta{_j} } J(\Theta{_0},\Theta{_1}) (for j = 0, 1) $
$ \Theta $ 값을 동시에 업데이트해야 된다는 것에 주의해야 한다.
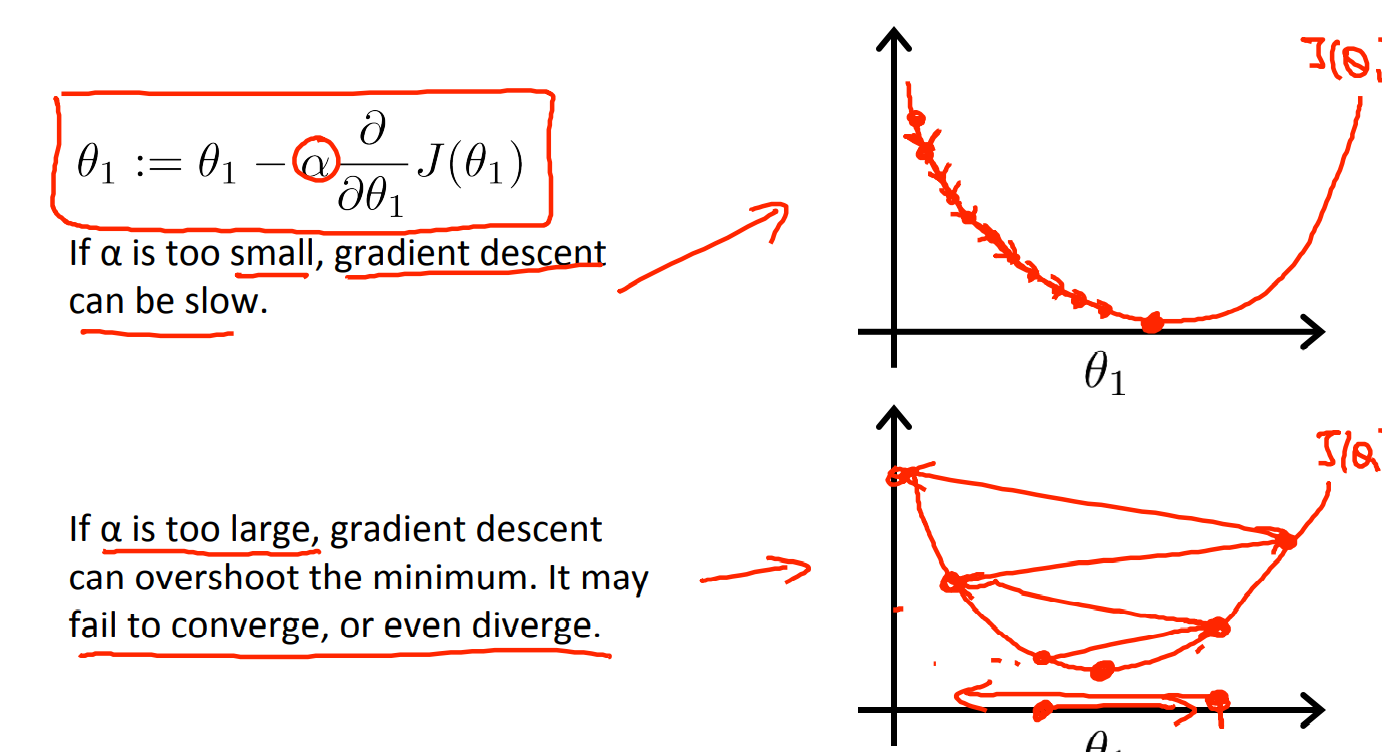
$ \alpha $는 learning parameter이고, 아래 그림과 같이 영향을 끼친다.
'머신러닝 > Machine Learning(Ng)' 카테고리의 다른 글
| [5주차] Neural Network - 2 (0) | 2021.08.14 |
|---|---|
| [4주차] Neural Network (0) | 2021.08.11 |
| [3주차-2] Regularization (0) | 2021.08.10 |
| [3주차- 1] Classification, Logistic Regression (0) | 2021.08.10 |
| [2주차] 다변수 선형 회귀, Normal Equation (0) | 2021.08.07 |