AI

※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습' 및 '[유튜브]혁펜하임의 트이는 강화학습'을 학습하고 작성한 글입니다. 

이제 본격적으로 강화학습 알고리즘 알고리즘인 SARSA와 Q-Learning 에 대해 살펴보자.

1. SARSA

먼저 앞서 살펴 본 시간차 예측에서, 가치함수 업데이트 수식을 살펴보자.

$ V(s) \leftarrow V(s) + \alpha (R_{t+1} + \gamma V(S_{t+1} - V(s)) $ 

시간차 예측 가치함수 업데이트 수식

SARSA는 기본적으로 위 수식을 기반으로 한다.

여기에서 아래와 같은 2가지 특징을 갖는다.

(1) Q 함수를 이용한다.

(2) 정책은 $ \epsilon $ - greedy 정책을 이용한다.

1. (1) SARSA 학습 과정

위에서 살펴보았듯, SARSA는 Q 함수, 행동 가치함수를 통해 학습한다.

이를 수식으로 나타내면 다음과 같다. 

$ Q(s, a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s, a))$

SARSA 큐함수 업데이트 수식

업데이트에 사용되는 값이 $ S, A, R, S_{t+1}, R_{t+1} $ 라서, SARSA 알고리즘이라고 부른다. 

그런데 여기서, 행동은 어떤 행동을 선택하게 될 까? 

즉, 정책이 무엇인지 궁금하다.

앞서 말했듯이 $ \epsilon $ - greedy 정책을 이용한다.

1. (2) $ \epsilon $ - greedy 정책

먼저 greedy 부터 살펴보자. 가장 좋은 것을 고르겠다는 의미이다.

즉, 기본적으로는 Q(s, a)가 가장 큰 행동을 취하면 된다.

다음으로 $ \epsilon $의 개념을 살펴보기 전에 먼저 다음 예시를 보자.

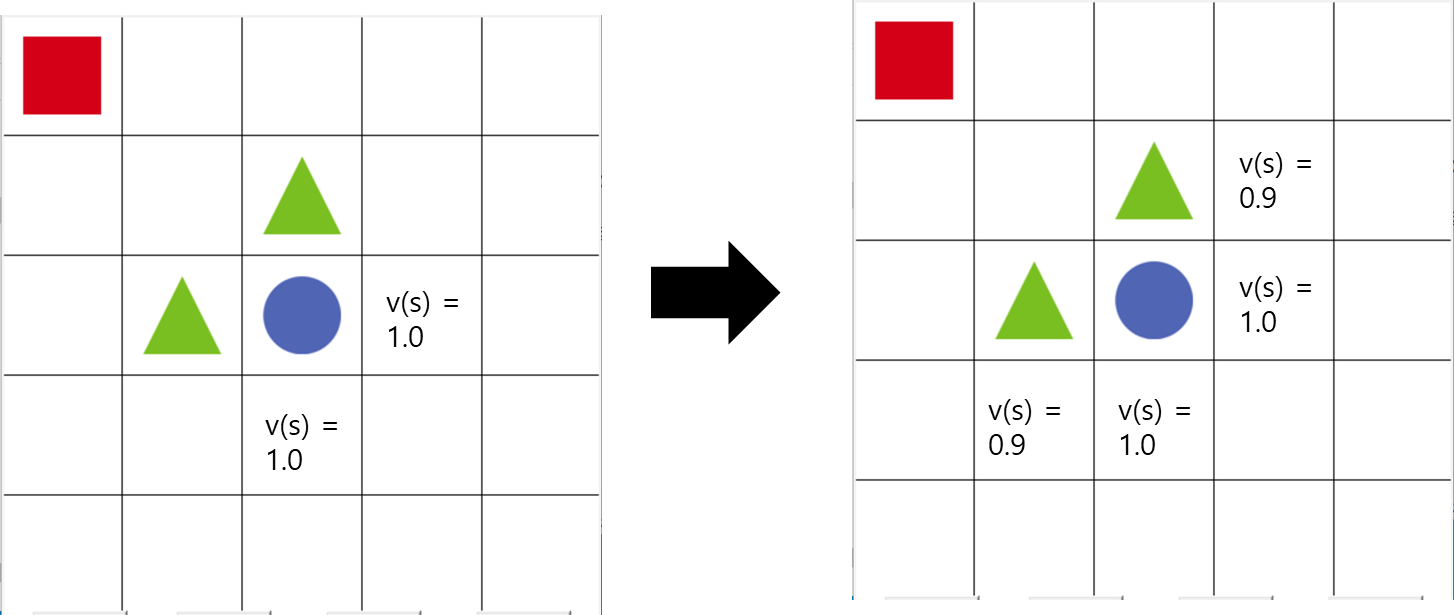
학습 초반 Q 함수는 랜덤하고 균등하게 분포되어 있을 것이다.

이 과정에서 우연히 위와 같은 코스를 반복해서 간다면, s = (0, 0)에서 Q(s, a)를 최대화하는 행동은 '아래로 이동'일 것이다. 

이렇게 한번 설정이 되어 버리면, greedy 정책에 의해 계속해서 이 길만 선택하게 된다. 

하지만 실제로 최적의 루트는 '오른쪽으로 이동'하는 것이다.

이런 문제를 예방하기 위해, $ \epsilon $의 개념이 등장한다.

기본적으로는 greedy 하게 이동하되, $ \epsilon $의 확률만큼은 랜덤하게 움직이는 것이 $ \epsilon $ -greedy 정책이다.

이때 랜덤하게 움직이는 것을 '탐험' 이라고 하고, 최적의 정책을 찾기 위해 중요하다. 

1. (3) 의사코드

SARSA 학습 과정을 간단하게 의사 코드로 표현해보자.

action = get_action(state) #epsilon greedy 기반 행동 추출
cur_q = q_table[state][action]

next_state, reward = do(state, action) # 환경에 의해 결정
next_action = get_action(next_state)

next_q = q_table[next_state][next_action]

td = reward + discount_factor*next_q - cur_q

q_table[state][action] = q_table[state][action] + step_size*td

$ Q(s, a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s, a)$

SARSA 큐함수 업데이트 수식

기본적으로는 위 수식을 코드로 표현한 것이다.

next_state가 환경에 의해 달라질 수 있다는 점과, 

next_action을 고를 때에도 $ \epsilon$-greedy 정책에 기반한다는 점에만 유의하면 된다.

2. 큐러닝, Q-Learning

2. (1) 큐러닝 업데이트 수식

큐러닝 역시 시간차 예측 기반의 알고리즘이고, SARSA와 거의 유사하지만 다음의 차이가 있다.

현재 상태에서는 $\epsilon$-greedy 정책을 통해 행동을 선택하고, 다음 상태에서는 가장 큰 큐 함수를 이용한다.

SARSA에서는 $ a_{t+1}$ 또한 $ \epsilon $-greedy 정책을 사용하여 현재의 가치 함수를 업데이트했다. 

Q-Learning에서는 그냥 가장 큰 $ Q(s_{t+1}, a_{t+1} $을 사용하여 현재의 가치 함수를 업데이트한다.

수식으로 비교하면 다음과 같다.  

$ Q(s, a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s, a)$

SARSA 큐함수 업데이트 수식

$ Q(s, a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma max_{a'}Q(s_{t+1}, a') - Q(s, a) $

큐러닝 큐함수 업데이트 수식

(※ 여기서 $ max_{a'}Q(s_{t+1}, a') $는, a'을 선택하겠다는 것이 아니라, 그냥 가장 큰 Q 함수를 그대로 사용하는 것이다.)

수식 상으로는 큰 차이는 없어보이지만,

이 간단한 차이로 인해, SARSA는 on-policy, 큐러닝은 off-policy가 되고, 꽤나 큰 차이를 불러온다.

이에 대한 내용은 뒤에서 다시 정리하고, 큐러닝 학습 의사코드를 먼저 살펴보자.

2. (2) 큐러닝 의사코드

action = get_action(state) #epsilon greedy 기반 행동 추출
cur_q = q_table[state][action]

next_state, reward = do(state, action) # 환경에 의해 결정

next_q = max(q_table[next_state]) # next_action을 굳이 뽑을 필요가 없다. 

td = reward + discount_factor*next_q - cur_q

q_table[state][action] = q_table[state][action] + step_size*td

수식도 그렇듯, 의사코드 또한 거의 비슷하다.

차이가 발생하는 부분은 next_q를 구하는 과정이다.

SARSA에서는 next_action을 $ \epsilon $-greey 정책으로 선택한 후, next_state와 next_action 의 Q 함수를 next_q 로 이용했다.

큐러닝에서는 next_action을 추출하는 과정이 없다. next_state 만 알면, next_state에 대한 Q 함수 중 가장 큰 값을 그대로 이용한다. 

3. 온-폴리시 vs 오프-폴리시

SARSA와 큐러닝의 학습 원리를 다시 살펴보자.

'SARSA는 현재 상태와 다음 상태에서 모두 $\epsilon $-greedy 정책을 통해 행동을 선택한다.'

'큐러닝은 현재 상태에서는 $\epsilon$-greedy 정책을 통해 행동을 선택하고, 다음 상태에서는 가장 큰 큐 함수를 이용한다.'

이때 SARSA는 온-폴리시 알고리즘이고, 큐러닝은 오프-폴리시 알고리즘이다.

오프 폴리시가 무슨 의미인지 먼저 살펴보자. 

큐러닝처럼, 행동하는 정책과 학습할 때 사용하는 정책이 다른 경우를 오프 폴리시라고 한다.

온폴리시는 둘이 같은 경우를 의미한다.

각각 살펴보기 보다는, 온폴리시는 기존에 사용되던 방법이고, 오프 폴리시가 새로운 방법이라고 생각하면 이해하기 좋다. 

따라서 오프 폴리시가 왜 필요한지 위주로 알아보자. 

3. (1) SARSA의 문제점

SARSA에서 다음과 같은 상황이 발생했다고 해보자.

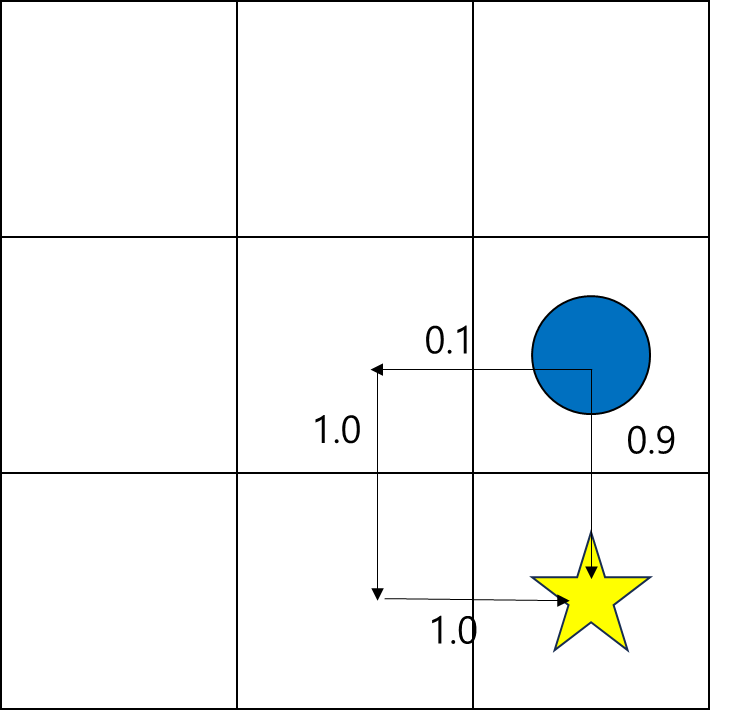
학습 초기에 랜덤하게 초기화 된 상황에서, 또는 학습 중이더라도 탐험에 의해 다음과 같은 이동이 발생했다. 

$ a_t$ 에서 오른쪽으로 이동하고, $ a_{t+1} $로 아래를 선택했더니 마이너스 점수가 발생했다. 

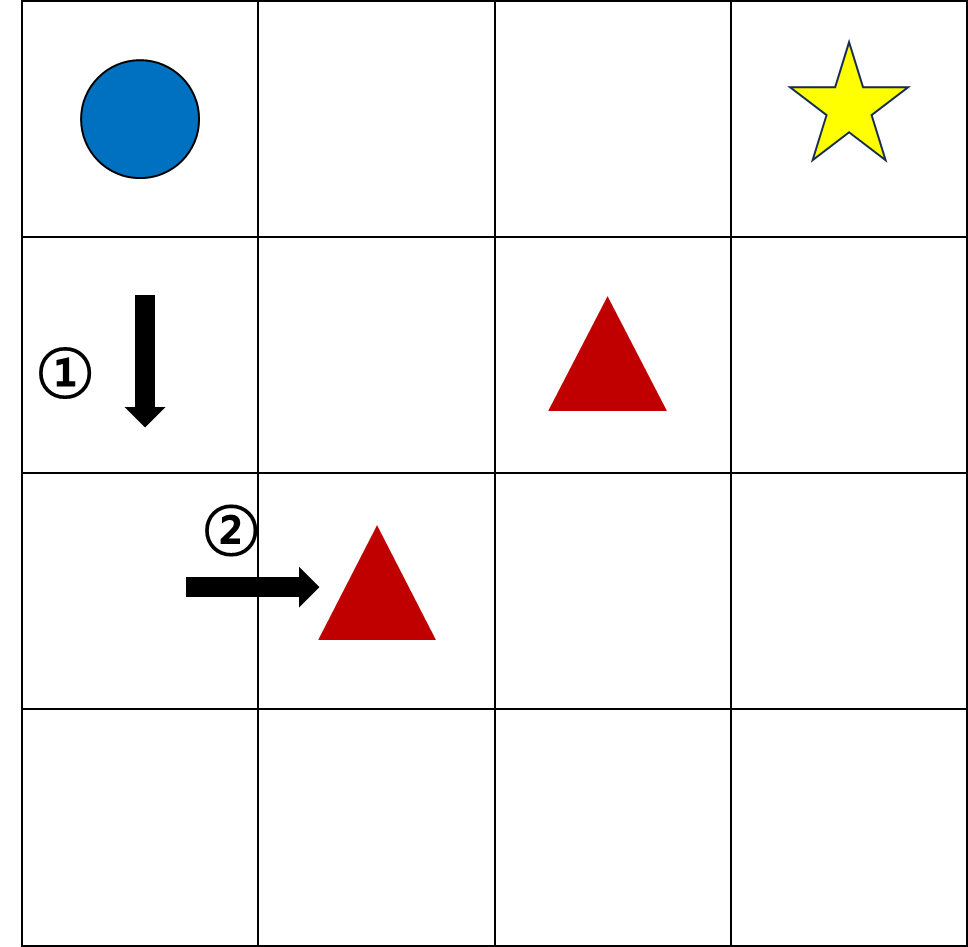
이 경우, s(0, 1)에서 오른쪽으로 이동하는 행동은 안 좋은 행동으로 평가된다. 

아래의 경우도 대칭적이므로 마찬가지이다.

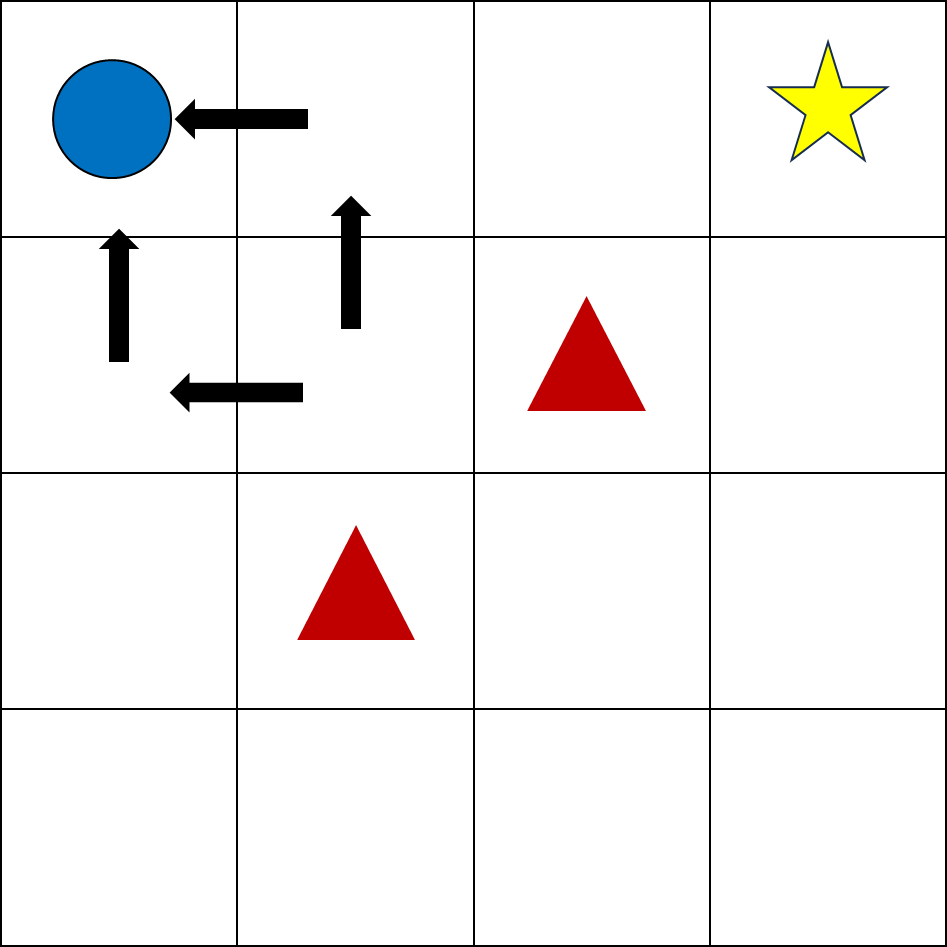
이렇게 되면 최악의 경우에는, 큐함수가 위와 같이 계산되어, 일종의 갇히는 현상이 발생한다.

물론 탐험에 의해 계속해서 학습하면 최적을 찾을 수 있겠지만, 어쨌든 학습이 길어지기 쉽다.

큐러닝에서는 이런 경우가 발생할까?  

큐러닝에서는 다음 행동에서는 $ max_{a'}Q(s_{t+1}, a')$ 을 통해 학습한다.

즉, 다음 행동은 제대로 행동하는 경우로 학습한다는 것이다. 

SARSA에서는 (0, 1) 에서 '우측으로 이동'을 선택한 후, $ a_{t+1}$을 고를 때 입실론 확률에 의해 잘못된 선택('아래로 이동')을 또 할 수 있다. 

그러나, 큐러닝에서는 그렇지 않다. 

따라서 위의 갇히는 예시는 발생하지 않는다.

3. (2) 직관적으로 차이 이해하기

바둑을 예시로 직관적으로 이해하는 것이 개인적으로는 더 도움이 되었다.

바둑에서 어떠한 한 수를 두고, 이 수를 평가하고 싶다. 

이 수가 좋은 수인지 평가하려면, 앞으로 둘 때도 올바르게 둬야 평가가 가능하다.

극단적인 예로, 알파고가 어떤 한 수를 계산하고 두더라도, 그 뒤로 유치원생이 이어받아서 두면 그 수를 분석하는 의미가 없어진다. 

SARSA에서는 어떤 수를 평가하려할 때, 가끔은 다음 수를 막 두기 때문에, 그 수를 잘못 평가하게 되는 경우가 있다.

반면 큐러닝에서는 적어도 평가하고 싶은 수 다음 수부터는 올바르게 둔다.

이것이 온폴리시와 오프폴리시의 개념적인 차이이다. 

3. (3) 오프폴리시의 장점

큐러닝에서는 다음 선택은 제대로 행동하는 경우로 학습한다.

따라서 다음과 같은 장점이 있다. 

(1) 지금의 행동을 보다 올바르게 평가할 수 있다. 

(알파고와 유치원생 반례를 생각해보면 된다.)

이때 사실은 $ max_{a'}Q(s_{t+1}, a')$ 도 계속해서 발전한다. 

따라서 같은 행동을 다시 하더라도, 평가가 달라질 수 있다.

예를 들어, 예전에는 나쁘게 봤던 수가 있다. -> Q(s, a) 

그런데 그 수 다음에 취할 수가 발전했더니 -> $ Q(s_{t+1}, a')$,

알고 보니 두면 좋은 수였다.  

와 같은 흐름이 가능한 것이다. 

즉, 

(2) 같은 행동에 대해서도 일종의 '재평가' 가 가능하다. 

추가로 큐러닝 말고 오프폴리시 자체는 다음과도 같이 이용이 가능하다고 하다.

현재 행동을 선택할 때는 내 선택 이용하고, 이후의 행동에 대해서는 상대방의 행동을 학습하면,

(3) 턴 방식의 문제에서 상대방의 정책에 맞춰 정책을 설정하는 것이 가능하다.

※ 주의

'오프-폴리시가 더 우월한 알고리즘이구나'라고 생각이 들었지만, 꼭 그렇지는 않다고 합니다.

구글은 온폴리시를 선호한다고 하고, OpenAI는 오프폴리시를 선호한다는 얘기가 있네요. 

정리

- SARSA는 시간차 예측 기반 on-policy 알고리즘이다.

- 큐러닝은 시간차 예측 기반 off-policy 알고리즘이다.

- Off-policy를 사용하면, 몇가지 장점이 있다. 

※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습' 및 '[유튜브]혁펜하임의 트이는 강화학습'을 학습하고 작성한 글입니다. 

앞선 글을 통해 다이나믹 프로그래밍을 통해서도 최적 정책을 찾아갈 수 있음을 확인했다. 

다만 모든 상황, 행동에 대한 제어, 계산이 가능해야 하므로 현실의 문제에 적용하기에는 무리가 있었다.

실제 사람은 어떤 새로운 것을 배울 때,

'우선 시도 -> 결과 -> 다시 방법을 업데이트' 의 순서로 학습한다.

이러한 아이디어를 구현하는 강화학습의 기초가 되는, 몬테카를로 예측과 시간차 예측에 대해 알아보자. 

1. 몬테카를로 예측

몬테카를로 예측은 가치 함수를 추정할 때, 충분히 많이 수행한 후 평균을 계산하는 방법이다.

i번째 시나리오에서, 어떤 상태 s를 지난 후 반환 값을 $ G_i(s)$라고 하면, s의 가치 함수를 다음과 같이 추정할 수 있다.

$v_\pi(s) \sim \frac{1}{N}\sum_{i=1}^{N}G_i(s) $

몬테카를로 가치함수 추정

N을 무수히 크게한다면, 매우 정확하게 가치함수가 계산될 것이다. 

여기서 한가지 수정하자면, 전부 다 해본 후 평균을 내는 것보다, 매번 조금씩 평균에 근사하도록 수정해가는 것이 좋을 것이다.

따라서 위 식을 수정해보자.

$ \frac{1}{N}\sum_{i=1}^{N}G_i(s) = \frac{1}{N}(G_N + \sum_{i=1}^{N-1}G_i) $

먼저 $ G_1 \sim G_N$ 까지의 합은, $ G_N + G_1 \sim G_{N-1}$의 합과 같으므로, 위와 같이 나타낼 수 있다.

여기서 식을 아래와 같이 변형해도 유효하다.

$ \frac{1}{N}(G_N + \sum_{i=1}^{N-1}G_i) = \frac{1}{N}(G_N + (N-1)*\frac{1}{N-1}\sum_{i=1}^{N-1}G_i)$ 

여기서 $ \frac{1}{N-1}\sum_{i}^{N-1}G_i $이 $ V_{N-1}$ 임을 이용하면, 최종적으로 다음과 같은 형태로 정리할 수 있다. 

$  \frac{1}{N}(G_N + (N-1)*\frac{1}{N-1}\sum_{i=1}^{N-1}G_i) = \frac{1}{N}(G_N + (N-1)V_{N-1}) $

$ = \frac{1}{N}(G_N + NV_{N-1} - V_{N-1}) $

$ = V_{N-1} + \frac{1}{N}(G_N - V_{N-1}) $

몬테카를로 업데이트 수식

이렇게 수식을 변형함으로써, 매 시나리오마다 가치함수를 업데이트할 수 있다.

이를 조금 더 일반화 할 수 있다.

$ \frac{1}{N}$ 대신 스텝사이즈, $ \alpha$의 개념을 이용하자. 

스텝사이즈는, 변화량을 얼마나 받아들일지 결정하는 0과 1 사이의 수로 설정하면 된다. 

또, $ V_N 과 V_{N_1} $대신 업데이트를 의미하는 '$ \leftarrow $' 로 표기하자.

그럼 최종적으로 다음과 같은 일반식을 얻을 수 있다.

$ V(s) \leftarrow V(s) + \alpha(G(s) - V(s)) $ 

몬테카를로 업데이트 일반식

여기서 $ G(s) - V(s) $ 를 '오차' 라고 표현하기도 하며,

앞으로의 많은 알고리즘도 위 형태를 기반으로 하니, 잘 확인해두는 것이 좋다.

이때 몬테카를로 예측에서는 반환값을 어떻게 계산할까?

몬테카를로 예측은 직접 해본 후 근사하는 방법이므로, 실제 에피소드가 종료될 때 얻은 반환값을 통해 계산한다.  

즉, 실시간이 아니다.

이는 에피소드가 끝나는 시점까지 기다려야 한다는 의미이므로, 에피소드가 긴 문제의 경우 적절하지 않다.

또한 실제로 사람도 학습할 때, 모든 결과가 나온 후에야 다시 확인하지는 않는다.

예를 들어 바둑을 둘 때, 승부가 난 후에 모든 수를 복기하는 것이 아니라, 실시간으로 한수한수 자신의 수를 평가한다.

2. 시간차 예측

이를 해결할 수 있는 중요한 아이디어가 시간차 예측이다. 

$ V(s) \leftarrow V(s) + \alpha(G(s) - V(s)) $ 

몬테카를로 가치함수 업데이트 수식

다시 가치함수 업데이트 수식을 보면, 이번에 얻은 반환값과 가치함수의 차이를 통해 계속해서 가치함수를 조정해간다.

이 수식의 형태는 그대로 유지하되, 반환값을 실제 반환값이 아니라 다음 타임스탭의 값만 이용하게 된다.

정확히는, 보상과 다음 상태의 가치 함수를 이용한다. 

$ V(s) \leftarrow V(s) + \alpha(R_{t+1} + \gamma V(S_{t+1}) - V(s))  $

시간차 예측 가치함수 업데이트

앞선 글에서 반환값을 통해 가치함수를 정의할 때의 개념을 그대로 적용하면 된다. 

이렇게 업데이트를 수행하면, 에피소드가 마치기 전에 실시간으로 가치함수를 업데이트할 수 있다는 장점이 있다. 

다만 다음 타임스탭의 가치함수, $ R_{t+1} + \gamma V(S_{t+1}) $ 자체가 초기에는 정확하지 않은 상태이므로 '이렇게 해도 수렴할까?' 하는 의문이 들 수 있다.

이에 대해서는 충분히 많은 반복속에서, 수렴한다는 것이 증명되어 있다고 한다.

앞으로 다룰 대부분의 알고리즘에서는 시간차 예측을 이용할 것이다.

대표적으로 다음 글을 통해 SARSA와 큐러닝에 대해 알아보자.

※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습'의 내용을 통해 작성한 글입니다.

1. 벨만 기대 방정식

이번 글에서는 다이나믹 프로그래밍을 통해 최적 정책을 찾는 방법을 알아볼 것이다.

이에 앞서 벨만 기대 방정식을 다시 살펴보자.

$ v_{\pi}(s) = E_{\pi}[R_t + \gamma v_{\pi}(s_{t+1}) | s] $

벨만 기대 방정식

여기서 실제로는 등호가 아니라, 대입 연산자를 적용하면, '참가치 함수'로 수렴한다.

이렇게 참가치 함수를 찾는 과정을, 다이나믹 프로그래밍을 통해 해결할 수 있다. 

2. 다이나믹 프로그래밍

다이나믹 프로그래밍은 큰 문제를 작은 문제들의 중첩으로 해결하는 방식이다.

가장 간단한 예시가 팩토리얼, '!' 연산 과정이다.

예를 들어, 1차원 배열 arr[n] = n!이 되도록 계산하고 싶다고 해보자.

for n in range(1, 100):
  value = 1
  for j in range(1, n):
    value = value*j
  arr[n] = value

가장 직관적인 구현은 위와 같을 것이다. 

이 경우의 시간 복잡도는 $ O(n^2) $이다.

그런데 생각해보면, 이전 문제의 답을 이용해 현재 문제의 답을 조금 더 쉽게 구할 수 있다.

예를 들어, 4! = 3!*4 이다.

즉, arr[n] = arr[n-1]*n 으로 간단하게 계산할 수 있다.

arr[1] = 1
for n in range(2, 100):
  arr[n] = arr[n-1]*n

코드 상으로는 위와 같고, 이 경우의 시간 복잡도는 $ O(n) $이다.

이처럼 다이나믹 프로그래밍을 적용하면, 작은 문제의 답을 통해 점점 더 큰 문제의 답을 효율적으로 구할 수 있다. 

※ 다이나믹 프로그램을 사용한다고 항상 시간 복잡도가 O(n)인 것은 아니다.

위의 팩토리얼 예시와 같은 경우를 bottom-up 방식이라고 하고, 반대로 top-down 방식도 존재한다.

예를 들어, arr[5] = 120을 기준으로 arr[4] = 120/5 와 같이 계산하면, top-down 방식을 이용했다고 생각할 수 있다. 

3. 그리드 월드에 적용하기

위와 같은 5x5 크기의 그리드 월드를 기준으로 생각해보자. 

이 예시에서는 빨간 네모가 이동하는 물체이고, 세모는 -1, 파란색은 +1의 보상을 의미한다. 

여기서 각 state의 가치를 다이나믹 프로그램으로 계산할 수 있다.

이때는 top-down 방식이 적용된다. 

다이나믹 프로그래밍에서는, 한 step에서 모든 상태에 대한 정보를 알고, 모든 상태의 가치를 업데이트한다. 

이를 의사코드로 나타내면 다음과 같다.

new_value = []

for state in states : # 모든 state
  new_value[state] = 0
  for action in actions: # 가능한 모든 action
    next_state = get_next_state(state, action)
    
    # 상태 가치 함수 계산 수식
    new_value[state] += get_policy(state, action)*(get_reward(state, action) + discount_factor*value[next_state])
    
value = new_value

상태 가치 함수 수렴 의사코드

※ 편의상 1차원 배열의 형태로 표현했다.

$ v(s) \leftarrow \sum_{a \in A}^{}{\pi (a|s)(r(s, a) + \gamma v(s'))} $

상태 가치 함수

위 수식을 코드로 표현한 것 뿐이다.

(매 state 별로 가치를 바로 업데이트 하지는 않고, new_value로 저장해두었다가 한 step이 지난 후 한번에 업데이트한다.)

다만 앞선 글에서 살펴봤듯이, 위 과정을 반복하면 참가치 함수로 수렴할 뿐이지, 최적 가치 함수를 찾는 것은 아니다.

따라서 이 방식에서는 최적 가치 함수를 찾기 위해 업데이트하는 과정도 존재해야 한다.

for state in states: # 모든 상태
  
  action_value_list = []
  policy = [0, 0, 0, 0] 
  
  for action in actions: # 모든 행동에 대해, 행동을 통해 얻는 가치를 계산
    next_state = get_next_state(state, action)
    reward = get_reward(state, action)
    
    action_value = reward + discount_factor*value[next_state]
    action_value_list.append(action_value)
    
  # 가치가 가장 큰 행동만 추출(동점 가능), 행동 확률 100%를 나눠갖기
  max_idx_list = get_index_of_max(action_value_list)
  prob = 1 / len(max_idx_list) 
  
  for idx in max_idx_list:
    policy[idx] = prob

정책 업데이트 의사코드

이후의 보상이 최대인 행동을 선택하는 방식으로 정책을 업데이트한다. 

이 두 가지 과정을 아래와 같이 적절하게 이용하면, 최적 정책을 찾을 수 있다.

1. 모든 상태에 대해 상태 가치 함수를 계산한다. 

2. 모든 상태에 대해, 보상이 최대인 행동을 선택하는 방식으로 정책을 업데이트한다.

3. 정책이 바뀌었으므로, 상태 가치 함수를 다시 계산한다.

4. 2~3 과정을 반복한다.

반드시 상태 가치 함수를 계산하는 과정과 정책을 업데이트 하는 과정을 1번씩 교차할 필요는 없다.

ex) 상태 가치 함수를 3번 계산하고, 정책을 업데이트 

이렇게 하면 최적 정책으로 수렴한다.

Top-down 방식을 이용한다고 했는데, 직관적으로만 살펴보고 넘어가자. 

가장 먼저 보상의 아래와 오른쪽에 있는 상태의 가치가 수렴할 것이다. 

정책을 업데이트할 때, 가장 초기 단계에서 최적 정책이 고정될 곳이 두 위치임은 자명하다. 

이렇게 수렴된 값을 기준으로 다시 주변 값들이 수렴하고, 최종적으로는 전체적으로 최적 정책에 수렴할 수 있다.

4. 다이나믹 프로그래밍의 문제점

다이나믹 프로그래밍으로도 최적 정책을 찾을 수 있다면, 왜 강화학습이 필요할까?

다이나믹 프로그램은 다음과 같은 한계를 지니고 있다.

① 계산량

매번 모든 state, 모든 action의 조합에 대해 계산하므로 계산량이 매우 많아진다.

물론 앞선 팩토리얼 예시나, 그리드 월드같은 경우라면 충분히 계산이 가능하지만, 

경우의 수가 많은 문제는 오래 걸리는 수준이 아니라, 풀 수 없다.

② 차원의 저주

①과 이어지는 얘기이다. state의 좌표가 z 축으로 한 축만 늘어난다고 하더라도, 경우의 수가 훨씬 늘어난다.

다양한 feature로 정의되는 현실의 문제는 state가 많을 것이고, 다이나믹 프로그램으로 해결할 수가 없다.

③ 상태에 대한 정보

위 예시에서는 보상이나 상태 변환 확률을 완전히 제어할 수 있는 상태였지만, 현실의 많은 문제는 그렇지 않다.

이 경우 다이나믹 프로그래밍을 통해 수렴하는 것 자체가 어려울 수 있다. 

정리

• 다이나믹 프로그래밍으로도 최적 정책을 찾을 수 있다.
• 그러나 현실의 많은 문제를 풀기에는 한계가 많다.
• 따라서 강화학습이 필요하다.

※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습' 및 '[유튜브]혁펜하임의 트이는 강화학습'을 학습하고 작성한 글입니다. 

1. 정책

앞선 글에서 MDP란 5가지 요소를 통해 순차적 의사결정 문제를 수학적으로 나타낸 것임을 알아보았다.

이렇게 MDP로 문제를 정의한 후, 결국 찾고자 하는 것은 최적의 정책을 찾는 것이다. 

먼저 정책에 대해 알아보자.

정책은 한 마디로, '어떤 행동을 선택할 것인가' 이다.

다시 그리드 월드를 통해 살펴보자.

원이 (0, 1) 위치에서 A = {상, 하, 좌, 우} 어떤 행동을 선택하는 것이 '최적 정책' 일까? 

당연히 '하'를 선택하도록 정책이 설정되어 있어야 될 것이다.

이처럼 정책은 특정 상태에서 어떤 행동을 할지 선택하는 것을 의미한다.

다만, 항상 위 예시처럼 항상 하나의 행동을 선택하는 것은 아니다.

예를 들어, (0, 0) 에서는 어떤 행동을 선택하는 것이 좋을까?

'우' 와 '하' 를 50%의 확률로 선택하는 것이 합리적일 것이다.

따라서 수학적으로 정책은 확률 분포라고 생각할 수 있다.

즉, 정책을 다음과 같이 특정 상태에서 선택할 행동의 확률 분포로 표현한다.

$ \pi(a | s) = P[a|s] $

정책

이 정책을 '최적'으로 설정하는 것이 강화학습이 풀고자 하는 문제이다.

2. 가치 평가 함수

정책을 '최적'으로 설정한다는 것이 어떤 의미인지 살펴볼 필요가 있다. 

각 상태에서 앞으로 받을 보상이 최대화 될 수 있는 선택을 하는 것이 '최적'일 것이다.

이때 특정 상태에서 앞으로 받을 보상을 다음과 같이 표현할 수 있다. 

$ G_t = R_t + \gamma R_{t+1} + \gamma^2R_{t+2} + ...$ 

반환값 (return)

(※ 할인률 $ \gamma $ 를 적용해야 함에 주의해야 한다.)

(※ 그리드 월드 예시에서는 끝에서만 보상을 받지만, 다른 문제에서는 중간중간 보상이 있을 수 있다.)

이러한 앞으로 얻을 보상의 합을 반환값(return) 이라고 표현하자.

이 반환값을 바탕으로, '상태'와 '행동'에 대한 가치를 평가할 수 있다. 

2. (1) 상태 가치 함수 (State Value Function)

먼저 상태에 가치가 있다는 표현 또한 그리드 월드 예시를 통해 살펴보자.

$ s_1, s_2$ 중 어떤 상태에 있는 것이 더 '가치' 있을까?

$ s_2$ 에 있는 것이 더 가치있다고 표현할 수 있다.

직관적으로는 그런데, 이를 수학적으로는 왜 그렇다고 제시할 수 있을까?

직관적인 부분인 표현을 더 구체화 해보면, 이렇게 생각했을 것이다.

'이 상태에 있으면, 보통 반환값이 더 높던데?'

이를 수학적으로는, '해당 상태에서의 반환값의 기댓값'으로 정의할 수 있다.

$ v(s) = E[G_t | s]$

가치 평가 함수

같은 상태라도, 상태 변환 확률이나, 정책의 분포로 인해 매번 받는 반환값은 달라지므로, 기댓값을 적용한다. 

앞선 예시를 조금 더 구체화해보자.

현재 정책은 위와 같이 설정되어 있다고 가정하자. 화살표는 행동을 선택할 확률(0~1)을 의미한다.

$ s_1$ 에서는 매번 같은 경로를 이동할 것이다.

총 4번 이동하여 보상을 얻을 것이므로 $ v(s1) = \gamma^3R$ 이 된다.

$ s_2$ 에서는 90% 확률로 R을 얻고, 10%의 확률로 $ \gamma^2R$을 얻는다.

즉, $ v(s2) = 0.9R + 0.1\gamma^2R$ 이다.

이제 수학적으로 왜 s2가 s1 보다 가치 있는 상태인지 표현할 수 있다. 

2. (2) 큐함수(Q-function), 행동 가치 함수

마찬가지로 행동도 그 행동을 했을 때 얻는 반환값의 기댓값으로 표현할 수 있다. 

행동 가치 함수는 큐함수라고 한다.

큐함수가 정책과 보다 직접적으로 연관이 있기 때문에, 실제로는 큐함수를 기준으로 학습을 진행하는 경우가 많다. 

$ q(s, a) = E[R_t + \gamma R_{t+1} + \gamma^2R_{t+2} + ... | s, a]$

큐함수

다시 이 예시를 살펴보자. 

s = (1, 2)에서 '하'로 이동하면 $ R$을 얻을 수 있다.

따라서 q(s = (1,2), a = '하') = R이다.

s = (1, 2)에서 '좌'로 이동하면, $ \gamma^2R$을 얻을 수 있다.

따라서 $q(s=(1, 2), a= '좌') = \gamma^2R$이 된다. 

2. (3) 상태 가치 함수와 큐함수의 관계

정책을 안다면, 상태 가치 함수를 큐함수로 표현할 수 있다.

$  v_{\pi}(s) = \sum _{a \in A}{\pi(a|s)q_{\pi}(s,a)} $

상태 가치 함수와 큐함수의 관계

즉, 어떤 상태의 가치는, 그 상태에서 취할 수 있는 행동의 가치(큐함수)의 가중 평균으로 표현할 수 있다.

말이 조금 복잡할 수도 있는데, 생각해보면 당연한 얘기이다.

다시 이 그림으로 돌아와서 s = (1, 2)의 가치를 생각해보면,

90% 확률로 아래로 이동하여 R을 얻고, 10% 확률로 왼쪽으로 이동하여 $ \gamma^2 R$을 얻을 수 있다.

따라서 $ v(s) = 0.9R + 0.1\gamma^2 R$이 된다.

이 표현 자체가, 아래로 이동하는 가치와 왼쪽으로 이동하는 가치의 가중 평균을 의미한다.

3. 벨만 방정식

3. (1) 벨만 기대 방정식

상태 가치 함수를 다른 방식으로도 표현할 수 있다. 

$  v_{\pi}(s_t) = E_\pi[R_t + \gamma R_{t+1} + ... | s_t] = E_\pi[R_t + \gamma v_\pi(s_{t+1}) | s_t] $

$  v_{\pi}(s_t) = E_\pi[R_t + \gamma v_\pi(s_{t+1}) | s_t] $

벨만 기대 방정식

반환값에서 직후의 보상인 $ R_t$를 제외한 나머지 항을 $ \gamma $ 로 묶으면, 다음 상태의 가치 함수가 된다.

생각해보면, 현재 상태가 현재의 보상 + 다음 상태의 가치인 것은 직관적으로도 합리적인 얘기이다.

이를 벨만 기대 방정식이라고 하고, 

벨만 방정식을 통해 현재 상태의 가치를 다음 상태의 가치로 표현할 수 있다.

큐함수 또한 벨만 기대 방정식으로 표현할 수 있다.

$ q(s_t,a_t) = E_\pi[R_{t} + \gamma q(s_{t+1}, a_{t+1}) | s_t, a_t] $

벨만 기대 방정식 - 큐함수

벨만 방정식이 중요한 이유는, 가치를 평가하는데 필요한 연산을 엄청나게 줄일 수 있기 때문이다.

계속해서 봤던 이 그림에서, 각각의 가치를 구하기 위해, 보상에 도달한 후에야 계산할 수 있었다.

표현을 편하게 하기 위해 정책을 간단하게 설정했지만, 정책이 조금만 복잡해져도 이 간단한 그림에서 조차 보상에 도달하는 경우의 수가 꽤나 많을 것이다. 

그러나 벨만 방정식을 이용하면, 인접한 바로 다음 상태의 가치만으로 현재의 가치를 판단할 수 있다. 

3. (2) 참가치 함수

$  v_{\pi}(s_t) \leftarrow E_\pi[R_t + \gamma v_\pi(s_{t+1}) | s_t] $

참가치 함수 수렴

사실 벨만 기대 방정식에서 등호가 성립하려면(참가치 함수), 충분히 수렴해야 한다.

따라서 실제 수렴 과정에서는 등호보다는 대입을 의미하는 '←'로 표현하는 것이 맞다.

※ 여기서, 경우의 수가 컴퓨터로 계산 가능한 수준이라면 다이나믹 프로그래밍 같은 계산으로도 참가치 함수를 찾을 수 있다. 

다만 현실의 문제를 해결하기 위해서는 계산이 어렵기 때문에, 강화학습을 사용하는 것이다.

단, 참가치 함수로의 수렴이 최적 정책을 찾는 것을 의미하지는 않는다는 것에 주의해야 한다. 

3. (3) 벨만 최적 방정식

다시 처음으로 돌아가서, 결국 찾고자 했던 것이 무엇이었는지 살펴보자.

최종적으로 구하고 싶은 것은 '최적 정책'이다. 

최적 정책은, 큐함수를 최대화 해주는 $ q(s_t, a_t)$가 최대인 행동을 선택하도록 하는 정책이다.

최적 정책 하에서 가치 함수를 수식으로 나타내면 다음과 같다.

$ v_*(s_t) = \textbf{max}_{a'}E[R_{t_1} + \gamma v_* (s_{t+1}) | s_t, a] $

$ q_*(s_t,a_t) = E_\pi[R_{t+1} + \gamma \textbf{max}_{a'}q_*(s_{t+1}, a_{t+1}) | s_t, a_t] $

벨만 최적 방정식

- * 는 최적 가치 함수를 의미한다. 

- $ \textbf{max}_{a} $ 은 뒤에 오는 수식을 최대화하는 $ a$을 선택하는 것을 의미한다. 

큐함수를 기준으로 좀 더 직관적으로 해석하면,

직후의 반환값 + 이동한 상태에서의 최적 행동을 선택했을 때 얻을 수 있는 가치 함수의 기댓값이 최적 큐함수이다.  

즉, 최적으로 이동한 후에도 최적의 선택을 하는 경우를 가치 함수를 정의하는 것이다.

최적 방정식에서도 결국 하나의 문제가 남아있다.

앞서 벨만 방정식을 이용하면, 한 단계 앞의 가치만 확인하면 된다고 했는데, 한 단계 앞의 가치를 알려면 결국엔 미래의 보상을 확인해야 한다.

결국 벨만 방정식 형태에서는, 일종의 시점 이슈가 재귀적으로 발생하는 것이다. 

이러한 문제를 극복하고, 최적 정책을 찾아가는 방법 중 하나가 강화학습이다.

3. (4) 수렴과 최적 탐색

벨만 방정식을 통해 참가치 함수로 수렴하는 것과, 최적 정책을 찾는 것이 나뉘어져 있어 헷갈린다.

실제로 벨만 방정식은 계산의 수가 적으면 다이나믹 프로그래밍으로도 수렴할 수 있다.

따라서 시점 이슈를 해결할 수 있다.

이 경우, 참가치 함수를 찾을 수 있고, 참가치 함수를 찾은 후 어떠한 방법(ex)greedy)으로 최적 정책을 찾는다.

즉, 실제로 2단계로 나눠진다.

계산의 수가 감당히 불가능한 수준이면, 참가치 함수로 수렴이 사실상 어렵다. 이 경우가 강화학습을 이용하게 된다.

이 경우 강화학습을 사용하면, 다이나믹 프로그래밍처럼 2단계로 나뉘지는 않는다. 

최적 정책을 찾아가는 여러 방법은 이후의 글에서 차차 알아볼 예정이다.

정리

• 보상의 합인 반환값을 통해 상태나 행동의 가치를 평가할 수 있다. (상태 가치 함수, 큐함수)
• 벨만 방정식을 통해 가치 함수를 다음 가치 함수만으로 표현하여, 연산을 줄일 수 있다.
• 벨만 방정식은 충분히 반복해야 참으로 수렴한다. 이후 최적 정책을 탐색할 수 있다.
• 현실의 문제는 참으로 수렴이 어렵고, 강화학습을 이용하여 최적을 찾는다.
  수렴과 최적 정책 탐색 2단계를 구분하지 않는다.