※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습' 및 '[유튜브]혁펜하임의 트이는 강화학습'을 학습하고 작성한 글입니다.
1. 정책
앞선 글에서 MDP란 5가지 요소를 통해 순차적 의사결정 문제를 수학적으로 나타낸 것임을 알아보았다.
이렇게 MDP로 문제를 정의한 후, 결국 찾고자 하는 것은 최적의 정책을 찾는 것이다.
먼저 정책에 대해 알아보자.
정책은 한 마디로, '어떤 행동을 선택할 것인가' 이다.
다시 그리드 월드를 통해 살펴보자.

원이 (0, 1) 위치에서 A = {상, 하, 좌, 우} 어떤 행동을 선택하는 것이 '최적 정책' 일까?
당연히 '하'를 선택하도록 정책이 설정되어 있어야 될 것이다.
이처럼 정책은 특정 상태에서 어떤 행동을 할지 선택하는 것을 의미한다.
다만, 항상 위 예시처럼 항상 하나의 행동을 선택하는 것은 아니다.
예를 들어, (0, 0) 에서는 어떤 행동을 선택하는 것이 좋을까?
'우' 와 '하' 를 50%의 확률로 선택하는 것이 합리적일 것이다.
따라서 수학적으로 정책은 확률 분포라고 생각할 수 있다.
즉, 정책을 다음과 같이 특정 상태에서 선택할 행동의 확률 분포로 표현한다.
π(a|s)=P[a|s]
정책
이 정책을 '최적'으로 설정하는 것이 강화학습이 풀고자 하는 문제이다.
2. 가치 평가 함수
정책을 '최적'으로 설정한다는 것이 어떤 의미인지 살펴볼 필요가 있다.
각 상태에서 앞으로 받을 보상이 최대화 될 수 있는 선택을 하는 것이 '최적'일 것이다.
이때 특정 상태에서 앞으로 받을 보상을 다음과 같이 표현할 수 있다.
Gt=Rt+γRt+1+γ2Rt+2+...
반환값 (return)
(※ 할인률 γ 를 적용해야 함에 주의해야 한다.)
(※ 그리드 월드 예시에서는 끝에서만 보상을 받지만, 다른 문제에서는 중간중간 보상이 있을 수 있다.)
이러한 앞으로 얻을 보상의 합을 반환값(return) 이라고 표현하자.
이 반환값을 바탕으로, '상태'와 '행동'에 대한 가치를 평가할 수 있다.
2. (1) 상태 가치 함수 (State Value Function)
먼저 상태에 가치가 있다는 표현 또한 그리드 월드 예시를 통해 살펴보자.

s1,s2 중 어떤 상태에 있는 것이 더 '가치' 있을까?
s2 에 있는 것이 더 가치있다고 표현할 수 있다.
직관적으로는 그런데, 이를 수학적으로는 왜 그렇다고 제시할 수 있을까?
직관적인 부분인 표현을 더 구체화 해보면, 이렇게 생각했을 것이다.
'이 상태에 있으면, 보통 반환값이 더 높던데?'
이를 수학적으로는, '해당 상태에서의 반환값의 기댓값'으로 정의할 수 있다.
v(s)=E[Gt|s]
가치 평가 함수
같은 상태라도, 상태 변환 확률이나, 정책의 분포로 인해 매번 받는 반환값은 달라지므로, 기댓값을 적용한다.

앞선 예시를 조금 더 구체화해보자.
현재 정책은 위와 같이 설정되어 있다고 가정하자. 화살표는 행동을 선택할 확률(0~1)을 의미한다.
s1 에서는 매번 같은 경로를 이동할 것이다.
총 4번 이동하여 보상을 얻을 것이므로 v(s1)=γ3R 이 된다.
s2 에서는 90% 확률로 R을 얻고, 10%의 확률로 γ2R을 얻는다.
즉, v(s2)=0.9R+0.1γ2R 이다.
이제 수학적으로 왜 s2가 s1 보다 가치 있는 상태인지 표현할 수 있다.
2. (2) 큐함수(Q-function), 행동 가치 함수
마찬가지로 행동도 그 행동을 했을 때 얻는 반환값의 기댓값으로 표현할 수 있다.
행동 가치 함수는 큐함수라고 한다.
큐함수가 정책과 보다 직접적으로 연관이 있기 때문에, 실제로는 큐함수를 기준으로 학습을 진행하는 경우가 많다.
q(s,a)=E[Rt+γRt+1+γ2Rt+2+...|s,a]
큐함수
다시 이 예시를 살펴보자.
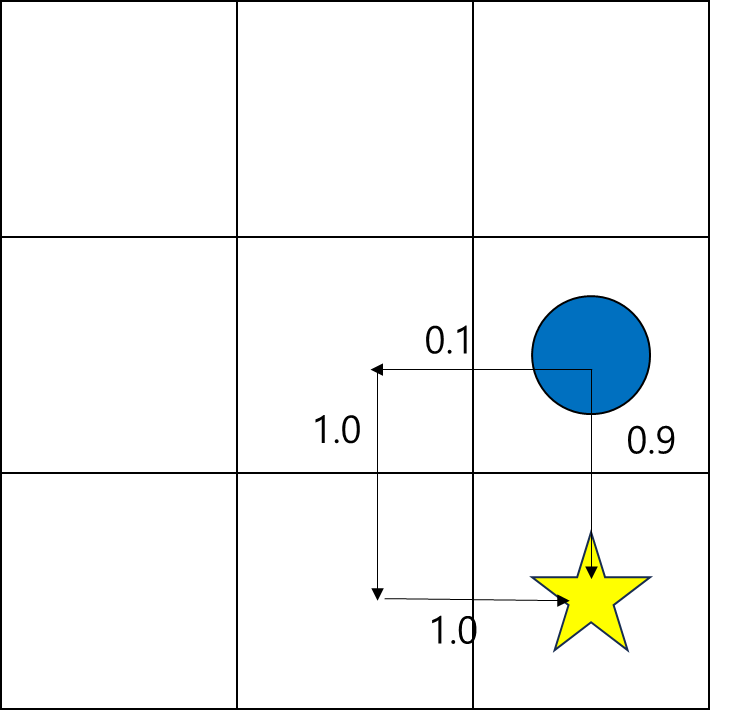
s = (1, 2)에서 '하'로 이동하면 R을 얻을 수 있다.
따라서 q(s = (1,2), a = '하') = R이다.
s = (1, 2)에서 '좌'로 이동하면, γ2R을 얻을 수 있다.
따라서 q(s=(1,2),a=′좌′)=γ2R이 된다.
2. (3) 상태 가치 함수와 큐함수의 관계
정책을 안다면, 상태 가치 함수를 큐함수로 표현할 수 있다.
vπ(s)=∑a∈Aπ(a|s)qπ(s,a)
상태 가치 함수와 큐함수의 관계
즉, 어떤 상태의 가치는, 그 상태에서 취할 수 있는 행동의 가치(큐함수)의 가중 평균으로 표현할 수 있다.
말이 조금 복잡할 수도 있는데, 생각해보면 당연한 얘기이다.

다시 이 그림으로 돌아와서 s = (1, 2)의 가치를 생각해보면,
90% 확률로 아래로 이동하여 R을 얻고, 10% 확률로 왼쪽으로 이동하여 γ2R을 얻을 수 있다.
따라서 v(s)=0.9R+0.1γ2R이 된다.
이 표현 자체가, 아래로 이동하는 가치와 왼쪽으로 이동하는 가치의 가중 평균을 의미한다.
3. 벨만 방정식
3. (1) 벨만 기대 방정식
상태 가치 함수를 다른 방식으로도 표현할 수 있다.
vπ(st)=Eπ[Rt+γRt+1+...|st]=Eπ[Rt+γvπ(st+1)|st]
vπ(st)=Eπ[Rt+γvπ(st+1)|st]
벨만 기대 방정식
반환값에서 직후의 보상인 Rt를 제외한 나머지 항을 γ 로 묶으면, 다음 상태의 가치 함수가 된다.
생각해보면, 현재 상태가 현재의 보상 + 다음 상태의 가치인 것은 직관적으로도 합리적인 얘기이다.
이를 벨만 기대 방정식이라고 하고,
벨만 방정식을 통해 현재 상태의 가치를 다음 상태의 가치로 표현할 수 있다.
큐함수 또한 벨만 기대 방정식으로 표현할 수 있다.
q(st,at)=Eπ[Rt+γq(st+1,at+1)|st,at]
벨만 기대 방정식 - 큐함수
벨만 방정식이 중요한 이유는, 가치를 평가하는데 필요한 연산을 엄청나게 줄일 수 있기 때문이다.

계속해서 봤던 이 그림에서, 각각의 가치를 구하기 위해, 보상에 도달한 후에야 계산할 수 있었다.
표현을 편하게 하기 위해 정책을 간단하게 설정했지만, 정책이 조금만 복잡해져도 이 간단한 그림에서 조차 보상에 도달하는 경우의 수가 꽤나 많을 것이다.
그러나 벨만 방정식을 이용하면, 인접한 바로 다음 상태의 가치만으로 현재의 가치를 판단할 수 있다.
3. (2) 참가치 함수
vπ(st)←Eπ[Rt+γvπ(st+1)|st]
참가치 함수 수렴
사실 벨만 기대 방정식에서 등호가 성립하려면(참가치 함수), 충분히 수렴해야 한다.
따라서 실제 수렴 과정에서는 등호보다는 대입을 의미하는 '←'로 표현하는 것이 맞다.
※ 여기서, 경우의 수가 컴퓨터로 계산 가능한 수준이라면 다이나믹 프로그래밍 같은 계산으로도 참가치 함수를 찾을 수 있다.
다만 현실의 문제를 해결하기 위해서는 계산이 어렵기 때문에, 강화학습을 사용하는 것이다.
단, 참가치 함수로의 수렴이 최적 정책을 찾는 것을 의미하지는 않는다는 것에 주의해야 한다.
3. (3) 벨만 최적 방정식
다시 처음으로 돌아가서, 결국 찾고자 했던 것이 무엇이었는지 살펴보자.
최종적으로 구하고 싶은 것은 '최적 정책'이다.
최적 정책은, 큐함수를 최대화 해주는 q(st,at)가 최대인 행동을 선택하도록 하는 정책이다.
최적 정책 하에서 가치 함수를 수식으로 나타내면 다음과 같다.
v∗(st)=maxa′E[Rt1+γv∗(st+1)|st,a]
q∗(st,at)=Eπ[Rt+1+γmaxa′q∗(st+1,at+1)|st,at]
벨만 최적 방정식
- * 는 최적 가치 함수를 의미한다.
- maxa 은 뒤에 오는 수식을 최대화하는 a을 선택하는 것을 의미한다.
큐함수를 기준으로 좀 더 직관적으로 해석하면,
직후의 반환값 + 이동한 상태에서의 최적 행동을 선택했을 때 얻을 수 있는 가치 함수의 기댓값이 최적 큐함수이다.
즉, 최적으로 이동한 후에도 최적의 선택을 하는 경우를 가치 함수를 정의하는 것이다.
최적 방정식에서도 결국 하나의 문제가 남아있다.
앞서 벨만 방정식을 이용하면, 한 단계 앞의 가치만 확인하면 된다고 했는데, 한 단계 앞의 가치를 알려면 결국엔 미래의 보상을 확인해야 한다.
결국 벨만 방정식 형태에서는, 일종의 시점 이슈가 재귀적으로 발생하는 것이다.
이러한 문제를 극복하고, 최적 정책을 찾아가는 방법 중 하나가 강화학습이다.
3. (4) 수렴과 최적 탐색
벨만 방정식을 통해 참가치 함수로 수렴하는 것과, 최적 정책을 찾는 것이 나뉘어져 있어 헷갈린다.
실제로 벨만 방정식은 계산의 수가 적으면 다이나믹 프로그래밍으로도 수렴할 수 있다.
따라서 시점 이슈를 해결할 수 있다.
이 경우, 참가치 함수를 찾을 수 있고, 참가치 함수를 찾은 후 어떠한 방법(ex)greedy)으로 최적 정책을 찾는다.
즉, 실제로 2단계로 나눠진다.
계산의 수가 감당히 불가능한 수준이면, 참가치 함수로 수렴이 사실상 어렵다. 이 경우가 강화학습을 이용하게 된다.
이 경우 강화학습을 사용하면, 다이나믹 프로그래밍처럼 2단계로 나뉘지는 않는다.
최적 정책을 찾아가는 여러 방법은 이후의 글에서 차차 알아볼 예정이다.
정리
- 보상의 합인 반환값을 통해 상태나 행동의 가치를 평가할 수 있다. (상태 가치 함수, 큐함수)
- 벨만 방정식을 통해 가치 함수를 다음 가치 함수만으로 표현하여, 연산을 줄일 수 있다.
- 벨만 방정식은 충분히 반복해야 참으로 수렴한다. 이후 최적 정책을 탐색할 수 있다.
- 현실의 문제는 참으로 수렴이 어렵고, 강화학습을 이용하여 최적을 찾는다.
수렴과 최적 정책 탐색 2단계를 구분하지 않는다.
'강화학습 > 강화학습 기초' 카테고리의 다른 글
| [강화학습 기초] SARSA 와 Q-Learning(큐러닝) (0) | 2023.08.14 |
|---|---|
| [강화학습 기초] 몬테카를로와 시간차 예측 (0) | 2023.08.13 |
| [강화학습 기초] 벨만 방정식과 다이나믹 프로그래밍 (1) | 2023.08.08 |
| [강화학습 기초] 강화학습과 MDP (0) | 2023.08.05 |