※ 본 글은 '[도서]파이썬과 케라스로 배우는 강화학습' 및 '[유튜브]혁펜하임의 트이는 강화학습'을 학습하고 작성한 글입니다.
1. 강화학습이란?
1. (1) 딥러닝과의 차이
강화학습에 대해 본격적으로 공부하기에 앞서, 강화학습이 어떤 것인지 살펴보자.
먼저 강화학습은 인공지능의 일부이다. 그러나 요즘 가장 일반적인 AI인 지도학습과는 다르다.
강화학습에 딥러닝 모델을 함께 사용하는 경우가 많긴 하지만(심층강화학습), 딥러닝 모델을 사용한다는 것이 지도학습을 사용한다는 의미는 아니다.

지도학습은 데이터와 정답(라벨)을 통해 모델을 학습시킨다.
비지도학습은 주어진 데이터 속에서 정답이 없이 학습한다.
강화학습은 주어진 데이터가 아니라, 주어진 환경 속에서 '보상'의 개념을 통해 에이전트가 스스로 학습한다.
(여기서 에이전트란, 딥러닝에서 모델을 의미한다고 생각하면 된다.)
1. (2) 그렇다면 왜 강화학습을 사용하는가
지도학습, 비지도학습, 강화학습이 각각 어떻게 동작하는지 간단하게 정리해봤다.
차이는 알겠는데, 최근엔 지도학습이 주류이다.
그렇다면 왜 강화학습을 이용할까?
강화학습을 통해 해결하고자하는 문제 자체가 다르기 때문이다.
강화학습에서 해결하고자 하는 문제는, 순차적으로 어떻게 행동할지 결정하는 것이다.
좀 더 구체적으로는 MDP(Markov Decision Process)로 정의되는 문제를 해결하는 방법 중 하나가 강화학습이다.
※ 순차적인 결정 자체는 RNN으로도 가능하지만, 강화학습은 MDP로 정의되는 문제를 해결한다는 점에서 차이가 납니다.
또한 엄밀히 MDP로 정의할 수 없는 문제더라도, 강화학습을 적용할 수 있고, 실제로는 RNN과 강화학습을 함께 사용하는 경우도 일반적이라고 합니다. 글 후반에 나오는 Markov 가정까지 살펴보면 이해될 것입니다.
여기서 MDP가 무엇인지 살펴보자.
2. MDP(Markov Decision Process)
2. (1) MDP란 무엇인가
앞서 강화학습은 MDP로 정의되는 문제를 해결하는 방법이라고 했다.
여기서 MDP란, 순차적 행동 결정 문제를 수학적으로 정의한 것이다.
MDP로 정의되기 위해서는 Markov 속성이 성립해야 한다.
Markov 가정에 대해 살펴보기 위해, MDP로 정의되는 문제의 구성요소를 먼저 살펴보자.
2. (2) MDP 구성요소
상태, 행동, 보상, 상태 변환 확률, 할인률
위 5가지가 MDP의 구성요소이다.
강화학습 기초 설명에 빠지지 않는 '그리드 월드'를 통해 각각에 대해 살펴보자.

위는 그림을 파란색 원을 이동하여, 별 위치에 도달하면 보상을 받는 그리드 월드이다.
① 상태 S - 환경 속 가능한 상태의 집합
말 그래도 주어진 환경 속 가능한 상태의 집합이다.
상태는 개발자가 직접 정의해야 한다. 핵심은 정의한 상태가 에이전트가 학습하기에 충분해야 한다.
위 그리드 월드에서는 보통 원의 현재 위치를 상태로 정의한다. 이를 다음과 같이 표현한다.
S = {(0, 0), (0, 1), (0, 2), (1, 0), ..., (2, 2)}
② 행동 A - 상태 S에서 선택 가능한 행동의 집합
어떠한 상태에 있을 때, 에이전트가 취할 수 있는 행동의 집합이다.
예를 들어, 위 그리드 월드에서는, 상하좌우로만 움직일 수 있다. 이를 다음과 같이 표현한다.
A = {상, 하, 좌, 우}
③ 보상 - 상태 s 에서 행동 a를 했을 때 주어지는 보상
시점 t에서 s 상태이고, a 행동을 취했을 때, 전달되는 보상을 $ R_t $ 라고 표현한다.
(경우에 따라 $ R_{t+1} $ 로 표현하기도 합니다.)
보상은 함수로 다음과 같이 표현하게 된다.
$ r(s, a) = E[R_{t} | s_t, a_t] $
여기서 기댓값의 개념이 적용된 이유는, 같은 행동을 하더라도 '환경'에 따라 그때그때 보상이 달라질 수 있기 때문이다.
④ 상태 변환 확률
상태 변환 확률은 용어만으는 와닿지 않는다.
상태 변환 확률이란, s에서 a라는 행동을 했을 때 s'에 도달할 수 있는 확률을 의미한다.
이는 환경에 의해 결정된다.
여전히 와닿지 않는데, 예를 드는 편이 낫다.
위 그리드 월드에 이상한 조건이 있다고 생각해보자.
(0, 0)에서 오른쪽으로 이동하는 행동을 선택하더라도, 매번 (0, 1)로 가는 것이 아니라, 10번 중에 1번은 (1, 0)으로 이동된다.
이처럼 행동이 같더라도 매번 같은 상태으로 변경된다는 것이 보장되지 않을 수 있으므로, 상태 변환 확률이 정의되어야 한다.
수식으로는 다음과 같이 표현한다.
$ P^{a}_{ss'} = P[s'|s_t, a_t] $
⑤ 할인률
할인률 역시 용어만으로는 와닿지 않는다. 예를 들어보자.
위 그리드 월드에서 보상을 R이라고 하고, 위치를 (1, 1)로 옮겨보자.
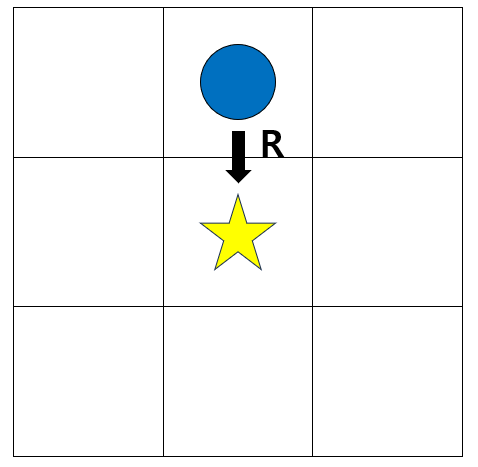
어느 시점 t에서 s = (0, 1) 이라면, 아래로 이동할 때 얻을 수 있는 보상은 R일 것이다. 즉, r((0,1) , '하') = R.
이는 명확하다.
그렇다면 다음은 어떨까?
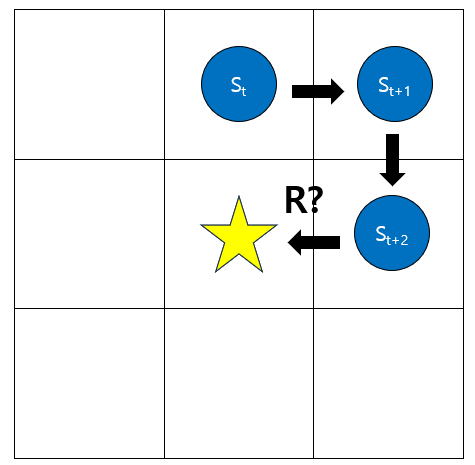
이렇게 돌아 가서 얻은 보상 역시 R 이라고 표현해도 될까?
느낌적으로만 생각해도, 이렇게 생각하면, 에이전트가 올바른 판단을 찾지 못할 것이 명확하다.
미래에 얻는 보상일 수록 일종의 패널티를 적용해야 한다.
이를 위해 할인률 $ \gamma (0 \leq \gamma \leq1) $ 를 한 단계마다 곱하게 된다.
따라서 위 경우, 얻은 보상은 $ \gamma^2R $로 판단해야 한다.
2. (3) Markov 가정
다시 돌아와서, 앞서 DMP로 정의하려면 Markov 속성을 만족해야 한다고 했던 내용을 살펴보자.
한마디로, 현재 상태가 중요하지, 현재 상태에 어떻게 도달했는지 중요하지 않아야 한다는 것이다.

이 상황을 다시 살펴보자. 사실 (0, 1)에 도달하기 까지는 어떤 과정이 있었는지 모른다.
(0, 0) 에서 우측으로 이동했을 수도 있고, 아니면 반시계 방향으로 한바퀴를 돌고 (0, 1)에 도달한 것일 수도 있다.
그러나 이 과정이 현재의 의사결정에 영향을 미치지 않는다. 어떻게 왔든, 아래로 이동하는 행동을 선택해야 하는 것은 명확하다.
위 경우를 수식으로 표현하면 다음과 같다.
$ r(s, a) = E[R_t | s_0, a_0, s_1, ..., s_t, a_t] = E[R_t | s_t, a_t] $
어떤 과정을 거쳐서 왔든, 현재 상태만 의사결정에 중요하다.
3. 정리
- 강화학습은 순차적 의사 결정 문제를 해결하는 방법이다.
- MDP는 순차적 의사 결정 문제를 5가지 요소를 통해 수학적으로 정의한 것이다.
- MDP로 정의하려면, 엄밀히는 Markov 속성을 만족해야 한다.
'강화학습 > 강화학습 기초' 카테고리의 다른 글
| [강화학습 기초] SARSA 와 Q-Learning(큐러닝) (0) | 2023.08.14 |
|---|---|
| [강화학습 기초] 몬테카를로와 시간차 예측 (0) | 2023.08.13 |
| [강화학습 기초] 벨만 방정식과 다이나믹 프로그래밍 (1) | 2023.08.08 |
| [강화학습 기초] 가치 평가 함수와 벨만 방정식 (0) | 2023.08.07 |