※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.
<Clustring>
Clustring은 Unsupervised learning의 대표적인 예시로, labeled 되어있지 않은 데이터를 특정 집단으로 분류하는 알고리즘이다. 즉 input data의 y가 주어지지 않는다.

supervised learning에서는 두 데이터의 label을 보고 그것을 잘 구분하는 decision boundary를 찾는 방식이였다면, unsupervised learning에서는 label은 주어지지 않고, 알고리즘 스스로 군집을 분류한다.
<K-means algorithm>
K-means algoritm은 clustring을 수행하는 대표적인 알고리즘 중 하나이다.
알고리즘의 원리는 다음과 같다.

우선 위와 같은 데이터를 가정한다.

다음으로 임의의 점 두 개(몇 개의 집단으로 분류할 것인지에 따라 다름)를 선택한 후 해당 점과 거리를 기준으로 데이터를 분류한다.
* 기준이 되는 점을 cluster centroids 라고 한다.
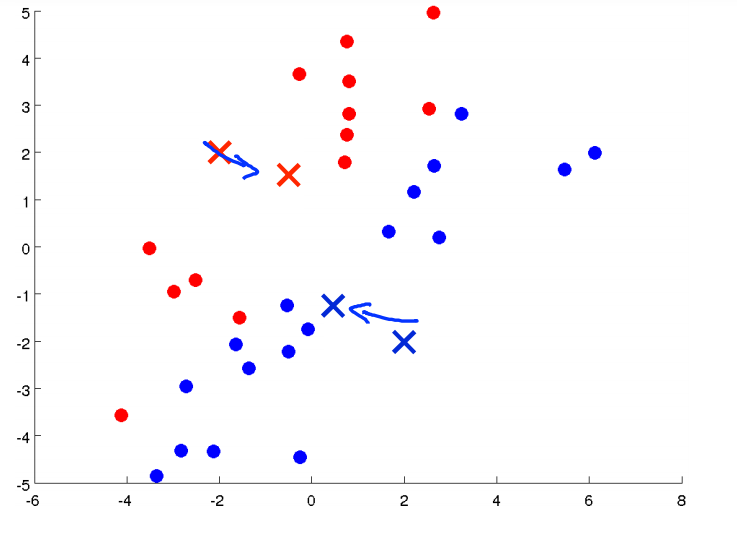
이렇게 데이터가 분류되고 나면, 다시 그 점들의 평균의 위치로 cluster centroids를 이동한다.


계속하여 같은 과정을 반복하다가 더 이상 centroid의 위치가 변하지 않는다면 clustering을 마친다.
* 분류가 잘 된 시점에서는 centroid가 변하여도 더 이상 clustering에 차이가 발생하지 않는다. 이 후 평균을 계산하여 centroid를 위치하면 점들이 바뀌지 않기 때문에 같은 값이 나온다. 따라서 clustering이 완료된 것이다.
위 과정을 확인하여 알고리즘의 동작 원리를 알 수 있다.
- K-means 구현
우선 K-means를 구현하기 위한 input은 2가지이다.
(1) 데이터( un-labeled)
(2) K (number of clusters)
K 또한 input으로 직접 선택해야 한다.

앞서 살펴본 알고리즘의 동작을 코드로 작성하면 위와 같다.
①로 표시된 반복은 각 데이터를 어떤 cluster로 분류할지 계산하고 $ c^{i}$로 저장하는 과정이다.
해당 데이터와 가장 가까운 centroid를 선택한다. (square값을 계산하는 것과 그냥 거리를 비교하는 것에는 큰 의미가 없다)
②로 표시된 반복은 cluster 별로 평균을 계산하여 다시 centroid를 선택하는 과정이다.
* 만약 어떤 데이터도 cluster-k로 선택되지 않았다면,
해당 cluster를 제거하거나, random initizaliztion하는 방법을 선택한다.(많이 발생하는 경우는 x)
위 과정을 centroid가 고정될 때까지 반복하면 된다.
- Optimization Objective
앞서 supervised learning에서도 항상 cost function을 정의했듯이,
K-means algoritm에서도 optimization objective, cost function이 존재한다.
알고리즘의 구현 과정에 cost function이 사용되진 않지만, cost function을 최적화하는 과정과 앞서 설명한 구현이 결국 같은 내용이다.
또한 cost function을 정의하면 알고리즘이 제대로 동작하는지 debug할 수 있다.
cost fuction은 다음과 같다.

K-mean algorithm에서 cost function을 distortion function이라고도 한다.
앞서 ①로 표시한 과정은 centroid를 고정시킨 상태에서 J를 최소화하는 과정이고,
②로 표현한 centroid를 평균으로 이동하는 과정에서도 J는 작아질 수 밖에 없다.
* 수학적으로 디테일하게 풀 수도 있지만 생략, 직관적으로도 이해할 수 있음
ex) (1, 0), (5, 0) 과의 거리 제곱의 합이 가장 작은 점은 그 평균인 (3, 0)임.
결론적으로, J는 알고리즘을 수행하는 과정에서 증가하는 경우가 발생하면 안된다.
(증가한다면 구현에 문제가 있는 것)
- Random Initialization
centroid를 임의로 초기화할 때, 조금 더 좋은 방법이 있다.
성능을 보장하는 방법은 없지만, input data 중에서 서로 다른 k개를 선택하는 방법이다.
그렇게하더라도 초기화를 어떻게 하는지에 따라 다음과 같은 문제가 발생할 수 있다.
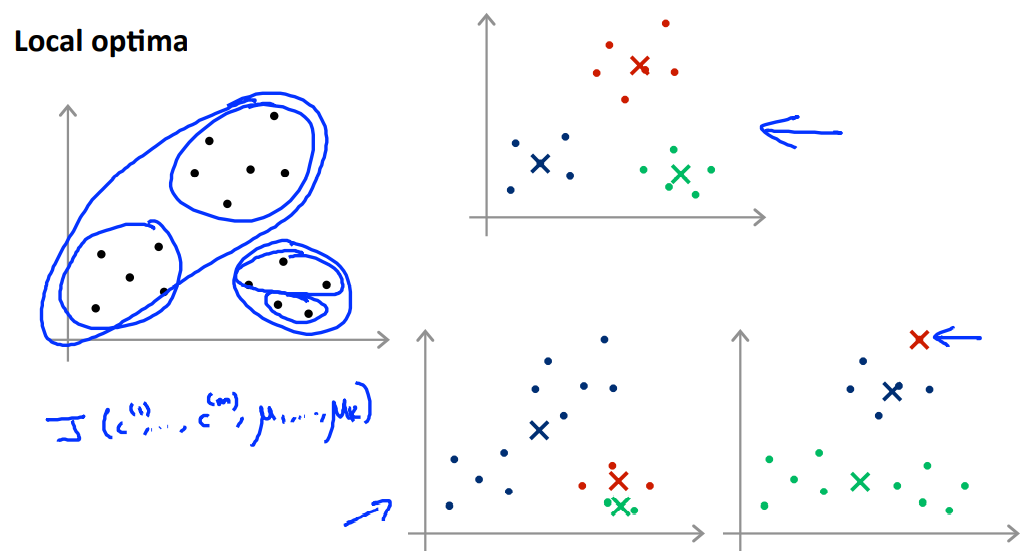
K-means 알고리즘은 local optima를 갖는다. 어떤 centroid로 시작하는지에 따라 다른 결과가 나올 수 있다.
그렇기 때문에 최선의 방법은 서로 다른 initialization에 대해 알고리즘을 여러 번 수행하는 것이다.
(대략 50-1000 times까지도.)
이렇게 하는 것이 항상 global optima를 보장하는 것은 아니지만 local optima를 찾더라도 꽤 낮은 J를 갖는 값을 찾을 가능성이 크다.
* K에 따라서도 차이가 있다. K가 작다면(2-10 정도) 여러번 적용해보는 것이 큰 향상을 줄 가능성이 크다.
K가 크다면 여러번 적용해보지 않더라도 처음부터 괜찮은 성능을 보여줄 가능성이 크다. 그렇기 때문에 여러번 적용할 경우 향상은 기대해볼 수 있지만 큰 차이는 없을 가능성도 크다.
- K, # of cluster 선택
앞선 예시들은 간단한 형태로 시각화를 통해 대략 어느 정도의 분류가 필요할지 확인할 수 있었다.
그러나 실제 데이터는 시각화가 쉽지 않은 경우가 많고, 또한 그렇게 하더라도 명확하게 몇 개의 cluster가 있다고 말하기 어려운 경우도 있다.
그렇다면 K는 어떻게 선택해야할까?
이 문제에 대해 명확한 해결책은 없지만 다음과 같은 점을 고려해 볼 수 있다.
(1) Elbow Method

한가지 방법은 Elbow method를 이용해보는 것이다. 위 그림의 좌측 그래프와 같이 변화량이 작아지는 지점을 선택하는 것이다. 그러나 오른쪽과 같은 그래프에 대해서는 적용할 수 없다.
* K가 증가할수록 J는 감소한다. 다만, local optima가 계산된 경우에서는 그렇지 않을 수 있다.
(2) purpose of clustering
clustering의 목표를 기준으로 K를 선택할 수도 있다.

예를 들어, 위와 같이 신체 조건에 따라 옷의 size를 clustring한다고 해보자.
clustring의 목표가 상품판매이고,
만약 5개의 size로 구분했을 때 판매량이 증가했다면, K=5로 선택할 수 있다.
또는 3개의 size로 구분했을 때 순수익이 더욱 증가하여 더 좋다고 평가한다면, K=3으로 선택할 수 있다.
K의 선택에는 automatic한 알고리즘이 없기때문에, 위와 같은 방법들을 적용해보는 것이 좋다.
'머신러닝 > Machine Learning(Ng)' 카테고리의 다른 글
| [9주차 - 1] Anomaly Detection (0) | 2021.08.23 |
|---|---|
| [8주차 - 2] Dimensionality Reduction, PCA (0) | 2021.08.22 |
| [7주차] Support Vector Machine (0) | 2021.08.19 |
| [6주차 - 2] prioritizing what to do, error matrix (0) | 2021.08.18 |
| [6주차 - 1] 모델 성능, Bias와 Variance (0) | 2021.08.16 |