※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.
Q4에서는 affine 계층 및 SVM, softmax loss를 layer로 구현한 후, layer들을 이어붙여 2-layer Neural Network를 구현하는 내용을 다룬다.
- Setup

이전 과제들과 마찬가지로 CIFAR10 data를 load하여 사용하고, shape는 위와 같다.
- Affine Layer (Forward/Backward)
● Forward
Affine layer의 forward 연산은 굉장히 단순하므로 코드는 생략하겠다.
N : 데이터의 수, D : 데이터의 차원, M : class의 수라고 할 때,
X = NxD, W = DxM 으로, X와 W의 곱만 수행하면 된다(+bias). 그 결과는 NxM 크기의 행렬이 된다.
● Backward
역전파의 경우도 사실 계산은 간단하기 때문에 코드는 생략하겠다.
X, W, b에 관한 미분을 각각 dX, dW, db 라고 하면

위와 같이 계산된다.
사실 affine 계층의 역전파 수식은 자주 쓰여서 알고 있었고, 또 shape를 맞추면 된다는 설명을 통해서 쉽게 기억할 수 있었다.
그러나 행렬과 행렬의 미분을 유도하는 과정은 쉽지 않았다.
(0) 행렬과 행렬의 미분?

가장 문제가 된 부분은 위와 같은 미분이다.
막상 유도를 하려다 보니 행렬과 행렬의 미분 자체에 대한 정의가 애매했다.
구글링을 해봐도 행렬과 행렬의 미분에 대한 정의가 명확하게 나온 자료가 없었고, 사실 수학적으로 명확한 정의가 없다는 내용도 있었다.
matrix-scalar 미분 -> matrix-vector 미분 -> matrix-matrix 미분 의 순서로 확장하면 미분을 정의할 수 있다고 한다.
그러나 계산 그래프를 이용하는 대부분의 경우에는 아래와 같이 행렬과 행렬의 미분을 적용하지 않고도 바로 역전파를 계산할 수 있다.
(1) L이 scalar인 경우

http://cs231n.stanford.edu/handouts/linear-backprop.pdf)의 자료를 바탕으로 이해했다.
(※ 이 부분에 대한 설명은 위 링크의 자료를 이용하였습니다.)
$\frac{\partial Y}{\partial W} $를 직접 계산하기 보단, chain룰을 이용한다.

간단하게 X와 W가 위와 같다고 하자.

$ \frac{\partial L}{\partial Y}$는 스칼라를 행렬로 미분하는 방법을 통해 얻을 수 있다.
스칼라를 행렬로 미분하는 방법을 몰랐더라도, 위 식을 보면 이해할 수 있을 것이다.


마찬가지로 $ \frac{\partial L}{\partial X}$도 식 (6)과 같이 나타낼 수 있고, $ x_{1, 1}$의 식에 집중하면 식 (7)과 같이 나타낼 수 있다.
(2개의 시그마가 붙는 이유에 대해서는 편미분을 확인하면 된다.)
다시 (7)의 식을 좀 더 직관적으로 표시해보면,

(10) -> (11)로 가는 과정이 이상하게 보일 수 있는데, 식 (7)의 시그마를 간단히 표현하기 위해 나타낸 것이라고 생각하면 된다.
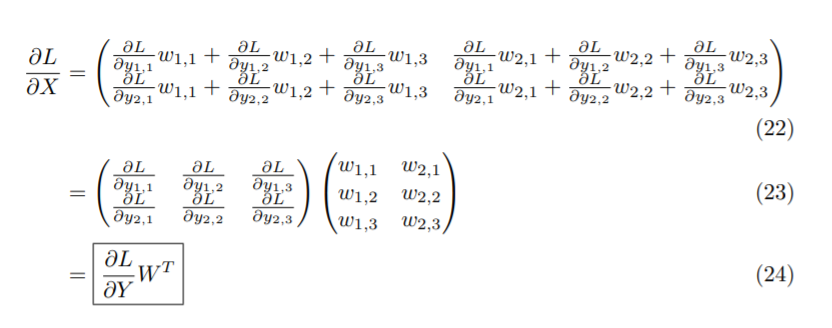
다른 경우에 대해서도 일반화해보면 $ \frac{\partial L}{\partial Y}$ 의 식은 유도할 수 있다.
- ReLU (forward/backward)
● Forward
마찬가지로 ReLU도 forward는 매우 간단하므로, 구현은 생략하겠다.
● Backward
Backward는 직관적으로 구현하긴 했지만,
활성화되는 경우는 그대로 전달되므로 미분값이 1, 그렇지 않으면 0으로 구현했다.
결국 정답은 맞았지만 이 부분도 행렬과 행렬의 미분이라 조금 더 생각해봐야한다.
- 기타 layers
추가로 softmax와 svm loss를 layer로 구현했다.
해당 부분은 Q2, Q3에서 다룬 내용과 거의 동일하므로 생략하겠다.
- 2-Layer Net
다음으로 앞서 구현한 layer들을 이용하여 2-layer network를 구현했다.

먼저 구현 내용을 계산 그래프로 구현하면 위와 같다.

코드로 구현한 내용은 위와 같다.
'dropout 계층 추가 실험' 주석 밑의 if문을 제외하면 앞서 계산그래프와 동일하다.
~_forward 연산은 앞서 구현했고 코드를 생략한 내용이지만 직관적으로 이해할 수 있을 것이다.
다만 반환값의 경우 (forward 연산값, input) 값이다. 역전파 계산시 필요한 값을 forward에서 return하고 cache_~ 로 저장하여 관리한다.
※ 수정 : Dropout의 출력이 잘못되어있다. Dropout을 적용할 시, test time에는 dropout확률을 곱해줘야한다.
● dropout
dropout은 뒷부분에서 튜닝을 통해 성능을 올리는 과제를 진행하는 과정에서 추가한 것인데, 코드가 나왔으므로 같이 살펴 보겠다.
먼저 계산 그래프로는 다음과 같다.

dropout 역시 하나의 layer로 생각하면 된다.
dropout에 대해서는 다음 그림이 잘 설명하고 있다.

학습 시에 random하게 일부 class에 대한(hidden layer일 경우라도 class라고 표현했다.) score를 비활성화하여(0으로 만들어서 없는 것처럼 동작) 줄여 과적합을 방지하는 기법이다.
코드를 보면 dropout이 True인 경우 random하게 선택된 class의 score를 0으로 만든다는 것을 확인할 수 있다.

다음으로 loss를 계산하고 미분값도 return하는 코드이다.
loss를 계산하면서 동시에 미분을 계산하는 방식으로 구현되어 있다.
미분은 각 layer마다 backward로 구현해두어서, 역전파 순서대로만 진행을 하면 된다.
dropout의 경우 drop한 class의 열에만 0을 곱해주면 된다.
(ReLU의 경우와 비슷하다.)
추가로 앞서 설명에 regularization term이 빠져있는데, 그 부분만 추가해주면 2-layer network가 완성된다.
(regularization term은 미분의 편리함을 위해 0.5를 곱해준다)
- train
다음으로 Solver class를 이용해서 train을 진행하는 내용이다.
Solver의 경우 train을 진행해주는 class로 model(앞서 구현한 2-layer network)과 데이터 그리고 기타 설정을 인자로 전달해주면 model을 학습시켜주는 class라고 이해하면 된다.
제공된 코드로 꽤 복잡하지만 우선 핵심적으로 다음 흐름만 이해하면 될 것 같다.
- init을 통해 여러 설정 초기화(learning rate, batch size 등등)
- train이 시작되면 매 iteration마다 step 호출
- step에서는 SGD를 활용하여 weight update

사용 자체는 매우 간단하다.
제공된 설명에 따르면 default 세팅으로 처음 train을 돌리면 대략 36% 정도의 validation 정확도가 나와야된다고 하는데, 기본설정에서도 40% 이상의 정확도가 나오긴했다.
(첫번째 실험 시에는 dropout을 추가하지 않았음.)


시각화 코드도 제공해서, 꽤 높은 퀄리티로 training process를 경험해볼 수 있다.
● Tuning
마지막으로 튜닝을 통해서 validation 성능을 48%이상으로 높이고 test 성능도 48% 이상 나오게 하라는 과제가 있었다.
다양한 수정을 해도 상관이 없다고 한다(ex) dropout).

최종 코드는 위와 같지만, 실험은 다음과 같이 진행했다.
1. learning_rate와 reg(regularization strength)와 num_epochs의 여러 조합에 대해 비교
2. 그 중 가장 좋은 model을 찾았지만 validation accuracy가 48%를 넘지 못했음.
3. 시각화 결과 과적합 문제가 있어서, dropout도 추가(2-Layer Net에 추가로 구현한 부분)
(Solver._step()에서 loss를 계산할 때(미분을 계산할 때) dropout 옵션을 True로만 설정하면 된다.)

그 결과 validation과 test에 대해 각각 50%와 49%의 정확도를 달성할 수 있었다.
최대 score가 52% 라고 한다.
'Computer Vision > cs231n' 카테고리의 다른 글
| [Lec5] Convolutional Neural Network (0) | 2022.01.09 |
|---|---|
| [cs231n] Assignment1-Q5 (0) | 2022.01.01 |
| [Lec 4] Backpropagation and Neural Network (0) | 2021.12.30 |
| [Assignment1 - Q3] Softmax (0) | 2021.12.30 |
| [Assignment1 - Q2] SVM (0) | 2021.12.30 |