[Assignment 2] Convolution 역전파, Spatial Batch Normalization

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

 

Assignment2 - Q4에서는 convolution layer, pooling layer를 구현하고, 최종적으로 CNN을 구현한다.

추가로 CNN에 특화된 batch normalization layer인  spatial batch normalization layer을 구현하는 내용 또한 다루고 있다.

 

그 중 convolution layer의 역전파 수식과 spatial batch normalization의 구현에 대해 정리해보겠다. 

 

<Convolution layer의 역전파>

Convolution layer의 역전파 또한 이전과 동일하게 chain rule을 이용해 계산할 수 있다. 

 

$ X = \begin{pmatrix}
x_{11}& x_{12} & x_{13}\\
x_{21}& x_{22} & x_{23}\\ 
x_{31}& x_{32} & x_{33}\\
\end{pmatrix},
W = \begin{pmatrix}
w_{11}& w_{12}\\
w_{21}& w_{22}\\
\end{pmatrix}, bias = b $,

 

간단하게 3x3 input과 하나의 2x2 filter 간의 convolution 연산을 살펴보겠다. (stride = 1, padding = 0)

위 예시만으로도 convolution 역전파 방식에 대해 파악할 수 있다. 

 

$Y = \begin{pmatrix}
x_{11}w_{11} +x_{12}w_{12} +x_{21}w_{21} +x_{22}w_{22} + b& x_{12}w_{11} +x_{13}w_{12} +x_{22}w_{21} +x_{23}w_{22} + b\\
x_{21}w_{11} +x_{22}w_{12} +x_{31}w_{21} +x_{32}w_{22} + b& x_{22}w_{11} +x_{23}w_{12} +x_{32}w_{21} +x_{33}w_{22} + b\\ 
\end{pmatrix} $

$ = \begin{pmatrix}
y_{11}& y_{12}\\
y_{21}& y_{22}\\
\end{pmatrix} $

 

$ dout = \begin{pmatrix}
\frac{dL}{dy_{11}}& \frac{dL}{dy_{12}}\\
\frac{dL}{dy_{21}} &\frac{dL}{dy_{22}} 
\end{pmatrix} $

위와 같이 연산의 결과는 y, 계산 그래프를 타고 전달되는 역전파의 값은 dout으로 나타냈다.

 

이제 $ \frac{dL}{dx_{21}} $의 계산을 살펴보겠다.

 

Chain rule에 의해 $ \frac{dL}{dx_{21}} $는 다음 수식으로 계산된다. 

 

$ \frac{dL}{dx_{21}} = \Sigma\Sigma{\frac{dL}{dy_{ij}} \frac{dy_{ij}}{dx_{21}}} $

 

이때 $\frac{dy_{ij}}{dx_{21}}$는 $ y_{ij}$의 계산에 $ x_{21}$이 포함되지 않은 경우 0, 포함된 경우는 $ x_{21}$과 곱해진 weight 이므로, ($ y$의 수식을 직접 미분)

위 수식을 풀어쓰면 다음과 같이 미분값을 얻을 수 있다.

 

$ \frac{dL}{dx_{21}} = \Sigma\Sigma{\frac{dL}{dy_{ij}} \frac{dy_{ij}}{dx_{21}}}
= \frac{dL}{dy_{11}}*w_{21} +\frac{dL}{dy_{12}}*0 + \frac{dL}{dy_{21}}*w_{11} + \frac{dL}{dy_{22}}*0 $

 

즉, $ \frac{dL}{dx_{21}} $는 '$ x_{21}$이 영향을 끼친(계산에 포함된) $ y_{ij}$의 역전파값($ \frac{dL}{d_y{ij}}$)과 그때 $ x_{21}$과 곱해진 weight의 곱의 합'이 된다.

 

전체 $ \frac{dL}{dx}$를 계산하기 위해서는 $ x_{21}$을 $ x_{rc}$로 일반화시키기만 하면 된다.

 

$ \frac{dL}{dw}$를 구하는 과정도 위 과정과 동일하다.

 

<Spatial Batch Normalization>

CNN에서 batch normalization을 적용하려면 mean과 std를 channel에 대해 계산해야 한다. 

 

channel 별로 통계를 내는 이유는 같은 channel이 같은 weight(filter)의 영향을 받았기 때문이다.

(과제에서 간단하게 소개된 개념이라, 자세한 개념은 실제 spatail batch normalization 논문을 참고하는 것을 추천합니다.)

 

Batch normalization의 구현도 복잡했기 때문에 구현에 앞서 걱정이 앞섰지만, 

주석으로 제공된 hint를 이용하여 비교적 간단하게 구현할 수 있었다.

 

앞서 구현한 batch normalization을 그대로 이용하면 된다.

다만 적용하기 위해 shape를 바꾸는 과정의 코드가 꽤 복잡했다.

3x3x2x2 matrix

위와 같은 3x3x2x2 (NxCxHxW) 크기의 matrix를 통해 처리 과정을 정리해보겠다.

대응되는 numpy array는 다음과 같다. 

'np.array(range(0, 36)).reshape(3, 3, 2, 2)' 를 통해 생성한 3x3x2x2 matrix이다. (N, C, H, W)

3x3x2x2 matrix

 

channel 별로 mean과 std를 구한 후 normalization을 수행해야 하므로, 

matrix를 다음과 같이 변경해야 한다. 

 

Vanilla Batch Normalization을 적용할 수 있는 matrix

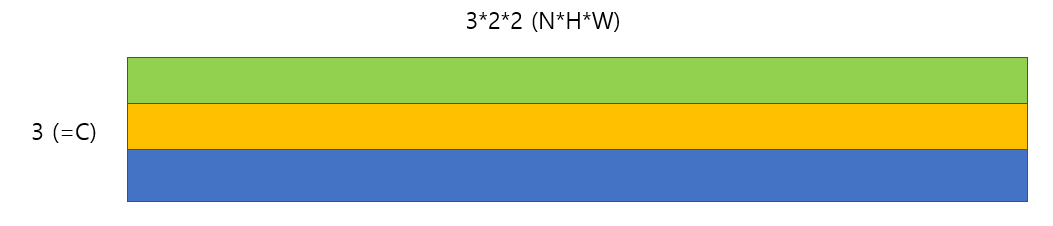
위와 같이 변경하면 각 row별로 일반적인 batch normalzation을 적용하면 된다.

Batch Normarlization 구현 상 row별로 하나의 데이터이므로, 정확히는 위 matrix에 transpose까지 적용해줘야 된다.

 

그러나 일반적인 reshape 만으로는 위와 같이 변경할 수 없었고,

reshape와 np.concatenate 두 가지 방식을 적용하여 변경이 가능했다.

 

먼저 reshape이다. 

NxCx(H*W)의 형태로 reshape하면 다음과 같이 변경된다. 

각 데이터 별로 channel의 matrix는 vector로 reshape되었다. 그림으로 나타내면 다음과 같은 상태이다.

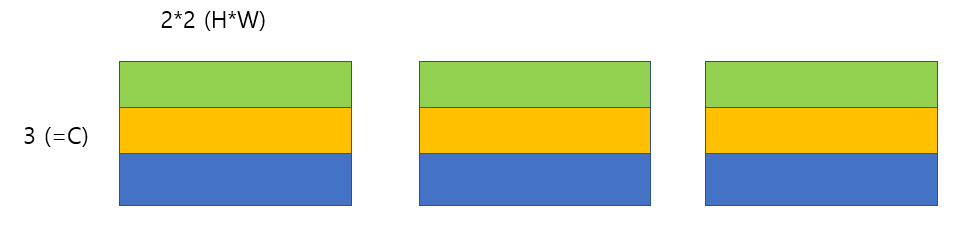
이제 3개의 결과를 row-wise로 이어붙여주기만 하면 되고, 해당 내용은 'np.concatenate( ~, axis = 1)' 코드로 구현이 가능했다.

 

Concatenate를 수행하고 trasnpose까지 적용한 결과이다. 

위 matrix에 대해서는 일반적인 batch normarlization을 적용할 수 있다. 

 

다만 그 결과를 다시 NxCxHxW shape으로 변경시켜주어야 하는데, 해당 내용은 반대의 순서대로 split과 reshape를 적용하면 된다.

최종 코드이다.

4줄의 코드로 spatial batch normalization의 구현이 가능하다.

 

Backward 연산의 경우에도 batchnorm_backward가 사용된다는 점을 제외하고 사실상 동일하다.