AI

※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.

<Neural Network>

- Non-linear classification

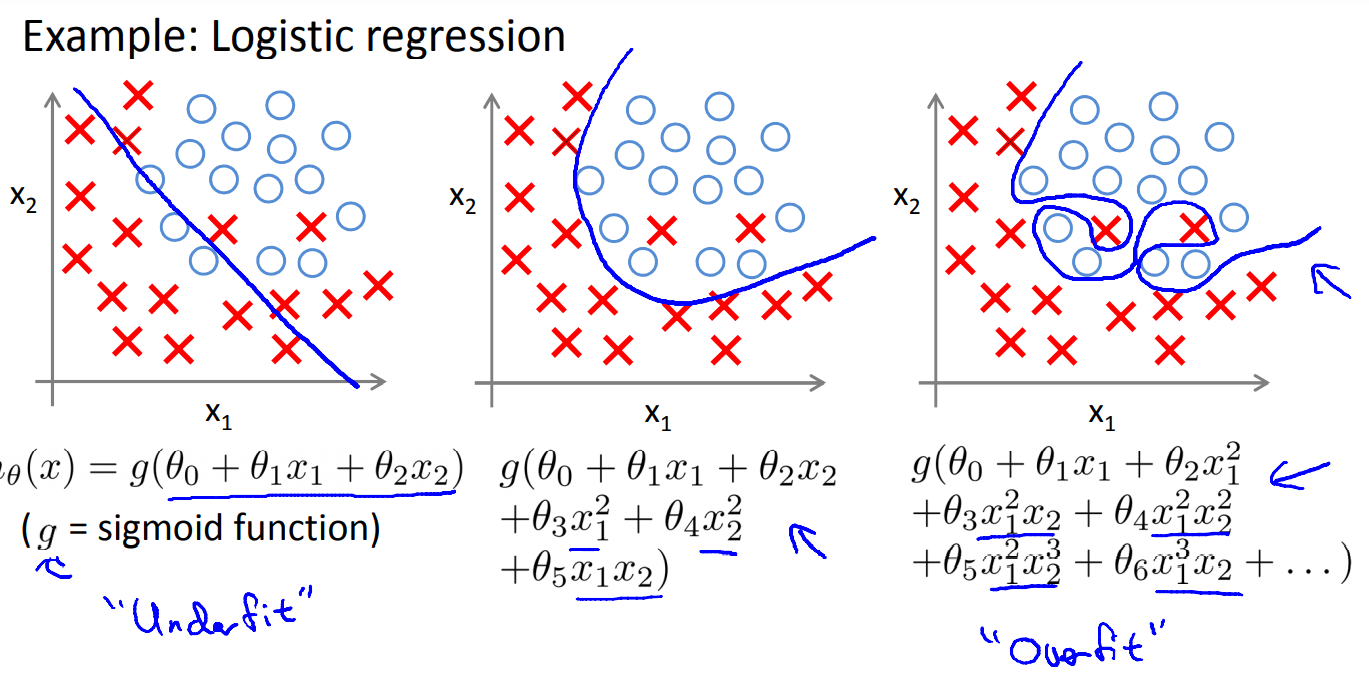
데이터를 항상 linear한 모델로는 설명할 수 없다.

이를 해결하기 위해 앞서 polynomial regression과 같은 방법을 이용하여 non-linear한 classfication을 수행하였다.

그러나 이러한 방식으로는 n개의 feature를 통해 대략 이차항의 조합만 추가하여도, $ \frac{n^{2}}{2}$개에 비례하는 새로운 feature를 만들게 된다.

3차항 이상의 조합까지 추가하면 feature의 수가 굉장히 많아져, 연산이 사실상 불가능하거나 지나치게 오래걸리게 된다. 

또한 이미지 처리의 경우 각 pixel 위치마다 feature로 처리하면,

간단하게 50x50 크기의 이미지만 처리하려해도 1차항으로 2500개의 feature가 나온다.(gray scale)

여기에 이차항 조합까지만 추가하려 해도 3 million 개의 feature가 나오게 된다.

- Neural Networks

따라서 Neural Network는 이러한 문제를 해결할 수 있는 non-linear 모델으로, 

실제 뇌의 뉴런 세포들의 동작을 mimic 하는 방식으로 학습하는 알고리즘이다. 

- 뉴럴 네트워크 구조

layer구조를 이루어, input layer와 output layer 그리고 그 사이의 hidden layers로 구성되어 있다. 

- input layer와 output layer는 이름 그대로 입력과 출력값을 의미하고, 그 외의 layer를 모두 hidden layer라고 한다.

- 노란색으로 표시된 unit 들이 하나의 뉴런에 대응된다고 보면 된다. 

각 뉴런에서 하는 일은 logisitic regression에서 하는 일과 동일하다. 즉 sigmoid function의 값을 계산하는데, 뉴럴 네트워크에서는 activation이라고 표현한다. 위 그림에서 $ a$로 표현된다. 

* $ a_{i}^{(j)} $는 j layer에서 i번째 unit의 activation을 의미한다. 

* bias unit은 항상 1의 값을 갖는 값으로, 계층의 0번째 activation으로 보면 된다. 그림에서는 생략하는 경우가 많다.

- 내부 동작(계산)

각 activation의 계산 과정을 자세히 살펴보면 다음과 같다.

* $ \Theta^{j} $는 matrix of weights를 의미한다. (뉴럴 네트워크에서 각 파라미터를 weights, 가중치로 표현한다.)

파라미터의 결정에 대해서는 이후에 다룬다고 한다.

어쨌든 위 식을 계산하려면, 슬라이드의 밑에 나와있는 것처럼 $ \Theta $는 $s_{j+1} \times (s{_j}+1) $ 크기의 matrix가 된다. +1은 bais unit에 의한 것이다.

식이 조금 복잡하기 때문에 다음과 z를 다음과 같이 정의하여 나타낼 수도 있다.

$ z{_{k}}^{j} = \Theta {_{k,0}}^{(j-1)}x{_0} + \Theta {_{k,1}}^{(j-1)}x{_1} + ... + \Theta {_{k,n}}^{(j-1)}x{_n}, $

vectorization을 적용하면 다음과 같다. input layer는 $ a^{(1)} $으로 취급하면 된다.

$ z^{j} = \Theta ^{j-1}a^{j-1} $ 

최종적으로 

$ a^{j} = g(z^{(j)}) $

와 같이 나타낼 수 있다. 

- 장점

위 그림과 같이 input layer를 가려본다면, layer 2를 input layer로 봐도 문제가 없다.

즉,  Neural Network 구조에서는 임의로 feature를 생성하지 않아도,

계속해서 새로운 feature를 learning한다고 볼 수 있다. 

- Simple Example

간단한 non-linear classification의 적용 예시는 다음과 같다.

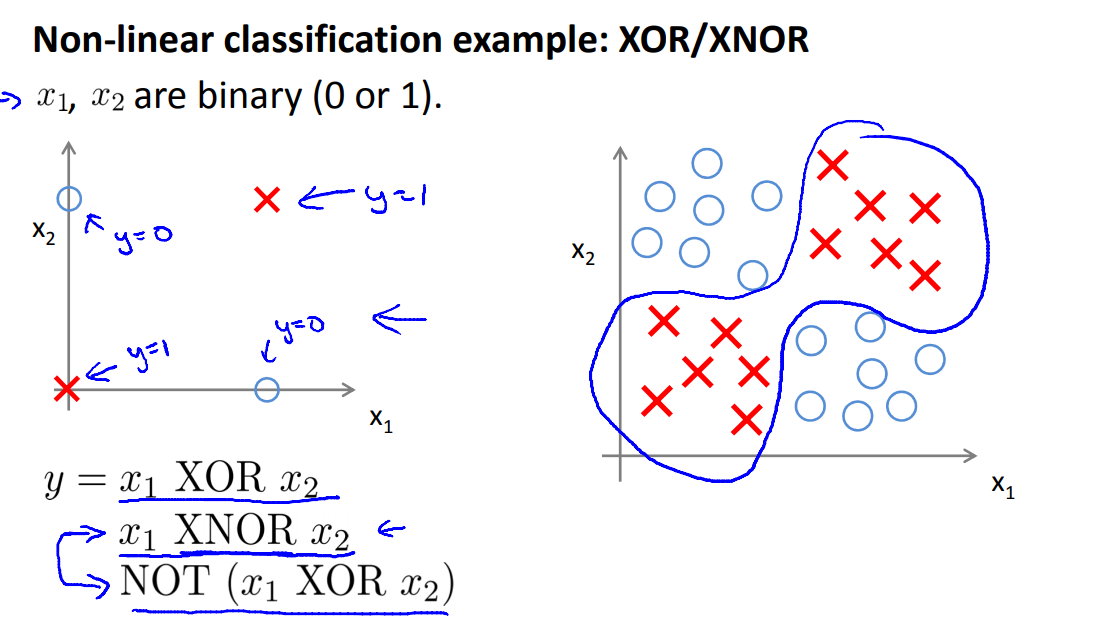
위와 같은 데이터를 분류하기 위해선, non-linear한 모델이 필요한 것을 알 수 있다.

참고로 x1 XNOR x2 연산을 통해 분류할 수 있다. 

우선 AND 로직은 위와 같이 가중치를 설정하여 계산할 수 있다. truth table을 통해 쉽게 이해할 수 있다.

최종적으로 위와 같은 구조를 통해 XNOR을 구현할 수 있다. 

(OR 등의 로직도 truth table을 통해 간단히 확인할 수 있으므로 생략)

이번 예시는 간단한 예시이지만, 이를 통해 

뉴럴 네트워크의 구조를 잘 설계하여 복잡한 로직의 처리도 가능하다는 것을 알 수 있다. 

- Multi-Class Classification

output layer의 unit을 1개가 아닌 여러개로 설저하고, output을 vector로 다루면 multi-class classification으로도 확장이 가능하다.

<Regularization>

- Regularization이란?

모델이 새로운 데이터를 접하더라도 좋은 예측 결과를 유지하도록 만드는 것.

즉, overfitting을 해결하는 것이다. 

overfitting이란 학습에 사용된 training 데이터에 지나치게 모델이 지나치게 적합되는 것으로, 

새로운 데이터에 대한 일반적 성능을 저하시킨다. (high variance)

linear regression과 logistic regression 두 경우 모두 발생할 수 있으며, 각 경우를 시각화한 그림은 다음과 같다.

반대로 underfitting 또한 존재한다 (high bias). underffiting이 일반적 성능을 향상시키는 것은 아니다.

- Overfitting을 해결하는 방법

위 슬라이드처럼 1. 불필요한 feature를 줄이거나, 2. regularization 기법을 사용하면 된다.

방법 1의 경우 유의미한 데이터를 버리게 될 수도 있고, 임의로 feature를 선택하기 어려울 수 있다.

(후에 selection 알고리즘을 다룬다고 한다.)

방법 2 regularization은 parameter의 magnitude를 줄인다고 나와있는데, 

이는 해당 특성이 모델의 결과값에 미치는 영향을 줄이는 것을 의미한다.

( 해당 특서에 대한 parameter 값이 작아지면 영향이 당연히 줄어든다. ) 

- Regularization, Cost Function

regularization을 설명한 슬라이드는 다음과 같다.

cost function에 파라미터를 포함시켜서 원하는 파라미터를 penalize 하는 방식으로 regularization을 구현하는 것을 확인할 수 있다.

cost function에서 파라미터 앞에 붙은 숫자 1000은 위 예시에서 임의로 붙인 숫자로, 일반적인 식에서는 람다로 표현한다. 일반적인 식은 다음과 같다. 

앞서 사용했던 cost function에 각 파라미터의 값을 추가하여 regularization을 구현한다.

보통 intercept를 제외한 모든 파라미터에 대해 하는 것이 일반적이다.

람다가 클수록 각 파라미터는 작아질 것이고, 

반대로 람다가 작다면 파라미터의 크기가 cost function에 미치는 영향이 작기 때문에 regularization이 잘 이뤄지지 않을 수 있다.

즉, fit-well 하는 것과 parameter를 줄이는 것(regularization) 는 trade-off 관계이며, 람다를 적절하게 설정해줘야 한다.

- Linear Regression Optimize (Gradient Discent, Normal Equation)

regularization을 고려하여 새로 정의된 cost function에서 최적 parameter를 찾는 과정도 동일하다.

(1) Gradient Discent

기본 알고리즘에서 cost function을 미분한 값만 변경하여 적용하면 된다.

그 결과 위와 같은 식으로 정리되고, 편미분 또한 어렵지 않게 할 수 있다.(생략)

주의할 점은 intercept parameter, j = 0인 경우는 regularization을 적용하지 않는다는 점이다.

(2) Normal Equation

결과적으로 Noraml Equation 수식은 다음처럼 바뀐다. 

기존의 Normal Equation이 각 파라미터에 대해 편미분한 값이 0이 되는 값을 찾는 것과 동일한 것처럼,

위 식도 같은 과정으로 유도된다고 한다.(생략)

참고로, m < n인 경우 $ X^{T}X $가 singular 하지만, 위 식을 적용하면 invertible 하다고 한다.(증명 생략)

즉, pinv가 아닌 inv만 제공하는 라이브러리 만으로도 적용할 수 있다. 

- Regularized Logistic Regression

Logistic Regression도 regularization이 필요하다. 

기본적인 원리는 동일하고, 수식만 logistic regressionn에 맞춰 적용하면 된다.

cost function

마찬가지로 기존 식에 파라미터의 값이 더해진다. 

Gradient Discent

위의 cost function을 편미분한 식만 달라진다. 편미분 과정 또한 어렵지 않다.(생략)

마찬가지로 j=0인 경우는 regularization을 수행하지 않는다.  

※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.

<Classification>

- Classification이란?

regression과 더불어 supervised learning의 대표적인 종류 중 하나로, 

개념적인 값으로 분류하는 것이다.

ex) 이메일이 스팸인지 아닌지, 종양이 양성인지 음성인지.

binary classificaiton과 multiclass에 대한 classification 모두 가능하다.

<Logistic Regression>

- hypothesis, 어떤 model을 사용할 것인지.

1. 선형모델? -> (x)

빨간 수직선 좌측의 데이터만 보면, 언뜻 선형 모델만으로 설명이 가능할 것처럼 보인다.

y = ax+b와 같은 직선을 찾고, 그 값을 기준으로 0.5 이상이면 양성 그렇지 않으면 음성으로 분류가 가능할 것 같다.

그러나 빨간 수직선 우측처럼 새로운 자료가 추가된다면 직선이 변화할 것이고 분류에 적합하지 않은 것을 확인할 수 있다. 

2. sigmoid/logistic function

따라서 classification 모델 중 Logistic regression model은 sigmoid function(= logistic function)을 사용한다.

수식은 다음과 같다.

$ h{_\Theta }(x) = g(\Theta ^{T}x) $

$ g(z) =  \frac{1}{1+e^{-z}} $

즉, $ h{_\Theta}(x) = \frac{1}{1+e^{\Theta ^{T}x}}$

그래프는 다음과 같이 그려지고, $ \Theta^{T}x $의 값으로 classification이 가능하다는 것을 확인할 수 있다.

sigmoid function의 특징은 다음과 같다. 

- 0 <= h <= 1

- 값은 Y = 1로 분류될 확률을 의미한다. (또는 1- h 는 Y = 0으로 분류될 확률)

(해당 내용에 대한 자세한 수학적 내용이 필요하다면, 다음 사이트를 참고.

https://towardsdatascience.com/why-sigmoid-a-probabilistic-perspective-42751d82686 )

- Decision Boundary

Decision Boundary는 해당 경계를 기준으로 분류가 달라지는 경계를 의미하고,

hypothesis의 값이 0.5가 되는 점들의 집합이라고도 볼 수 있다.

* Decision Boundary는 parameter에($ {\Theta}$) 의해 결정된다.

* $ {\Theta}$는 Cost Function을 기준으로 결정된다.

앞서 $\Theta^{T}x $의 값을 통해 분류가 가능했던 점을 생각하면서 위 식을 함께 보면

parameter에 의해 결정된다는 것을 알 수 있다.

선형회귀에서 polynomial regression을 통해 non-linear한 데이터를 모델링했던 것처럼 

Non-linear한 decsion boundary도 가능하다. 

- Cost Function

parameter를 결정할 때 cost function을 기준으로 결정하는 것은 regression과 동일하다.

그렇다면 Logistic Regression에서는 어떤 cost function을 사용해야 적절할까?

언뜻 생각했을 때 linear regression과 동일하게 사용해도 되지 않을까 싶지만,

결과적으로 말하자면 h(x)가 복잡한 형태이기 때문에 cost function이 non-convex하게 된다고 한다.

따라서 Cost로 다음과 같은 식을 이용한다.

그래프의 형태는 y=1인 경우만 나와있지만, 반대의 경우도 쉽게 생각할 수 있다.

예측이 정답에 가까울 수록 cost가 작아지면서, 위와 같이 정의하면 cost function이 convex하게 된다고 한다.

(자세한 수학적 증명은 생략)

최종적으로 J($ \Theta $) = Cost Function은 다음과 같이 정의된다.

안에 cost 식은 y가 0 또는 1인 점을 이용하여 하나의 식으로 표현되었다. 

- Gradient Discent

위 cost function은 convex하므로, 동일하게 gradient discent 알고리즘을 적용하여 최적의 parameter를 찾을 수 있다.

알고리즘의 내용은 동일하고, cost function만 바뀌어 적용했을 때,

최종적으로 파라미터를 업데이트하는 수식은 위와 같다.

(미분식은 생략, 해보면 알 수 있음)

*형태는 linear regression에서와 동일하지만, h(x)가 다르기 때문에 같은 식은 아니다.

위 과정을 구현할 때도 vectorization을 사용하면 유용하다.

또한 마찬가지로 업데이트 정도를 결정할 때 feature를 곱한 후 sum 하는 식이 포함된다.

따라서 linear regression과 동일한 이유로 feature scaling을 해주면 좋다.

- 기타 알고리즘

그 외에도 최적 파라미터를 찾는 다른 알고리즘이 존재하지만, 자세히 다루기에는 많은 시간이 들기 때문에 라이브러리에 대해서만 다룸.

위의 장점들이 필요하면 해당 라이브러리를 찾아보고 사용하면 된다.

- Multi-Class classification

앞서 말했듯이 binary 분류가 아니더라도 가능하다. 

결론적으로 말하자면 binary 분류의 내용을 그대로 one-vs-all 형태로 적용하면 된다.

ex)  0, 1, 2를 구분하고자 할 때,

0과 0이 아닌 데이터.

1과 1이 아닌 데이터.

2와 2가 아닌 데이터.

로 구분하여 각 데이터 별로 binary classificaiton 모델을 적용하면 된다.

각 모델이 각 클래스일 확률을 나타내고, 최종적으로 가장 높은 확률의 클래스를 선택하도록 구현하면 된다.

* 각 클래스로 분류될 확률을 나타내므로, 모델들의 h(x)의 값의 합은 1이다.

* 모델별로 $ \Theta $가 달라지기 때문에 헷갈리지만, 확률 관점에서 생각해보면 합이 1이 되어야 하는 것을 알 수 있다. 

* 파라미터가 다른 각 모델 별로는 독립이기 때문에, 그 합이 1이 될 필요는 없다.

x가 1일 확률이라는 것은 모델 1의 판단이 그렇다는 것이지, 실제로 어떤 input X가 1일 확률을 의미하지는 않는다.

- 정리 

각 식에 대해 간단하게 정리.

(1) h(x)는 1로 분류될 확률을 의미.

(2) decision boudary는 파라미터에 의해 결정.

(3) 파라미터는 cost function에 의해 결정.

- gradient discent 추가 내용

다변수 선형회귀에서도 동일하게 gradient discent 알고리즘을 이용하여 cost function을 최소화하는 파라미터를 찾을 수 있다.

선형회귀에 맞춰 gradient discent를 적용한 식은 위와 같다. hypothesis 대신 식을 풀어서 써본 다음 미분해보면 확인할 수 있다.

- Feature Scaling

각각의 feature들(x1, x2 , ..., x_n)이 동일한 scale을 갖도록 맞춰주는 방법이다.

이렇게 하면 gradient discent 알고리즘이 더 빠르게, 적은 iteration만으로 최적 parameter를 찾을 수 있다.

파라미터가 변경됨에 따라 cost function의 값이 변경되는 과정을 나타낸 그림이다.

왼쪽은 scale에 차이가 있는 경우, 오른 쪽은 거의 없는 경우이다. 

왼쪽의 경우 진동하며 더 많은 iteration이 필요한 것을 확인할 수 있다.

강의에서 이에 대해 수학적으로 자세히 풀지는 않았지만 직관적으로도 어느 정도 이해할 수 있다. 

우선은 feature scaling과 그 필요성에 대해 알아두는 것이 중요할 듯 하다.

* 일반적으로 -1 <= feature <= 1 정도로 통일하여 scaling하고, 근사적으로만 통일되어도 문제 없다고 한다.

- Mean Normalization

i번째 feature들의 평균으로 빼주는 것. feature들의 평균이 대략적으로 0이 된다.

보통 feature scaling과 mean normalization을 함께 적용.

- Gradient Discent의 debugging

앞서 Gradient Discent를 적용할 때 learning rate(알파)를 지나치게 크게 설정하면 최적값을 찾는 것에 실패한다는 점을 확인했었다. 

그렇다면 알고리즘이 제대로 동작하고 있는지 확인하려면 어떻게 해야할까?

위 그림처럼 알고리즘을 반복하면서 cost function값의 변화를 확인하면 된다.

cost function이 계속하여 감소하지 않고, 증가하거나 진동한다면 learning rate가 크게 설정되어 동작하지 않는 경우이다.

* 2차 함수에서 learning rate가 클 때 파라미터가 발산하는 그래프를 떠올리며 굳이 cost function이 아니라, 파라미터의 변화만 보고도 판단할 수 있지 않을까 생각했지만, 앞서 feature scaling에서 사용된 그림을 보면 feature가 많을 때 파라미터는 커지거나 작아지는 과정이 교차될수도 있음.

- Learning Rate 설정

Learning Rate를 설정하는 것은 debugging 과정을 그대로 이용하면 된다.

(1) 너무 클 경우 : debugging과정에서 제대로 동작하지 않는 것을 알 수 있다. 줄이면 된다.

(2) 너무 작을 경우 : iteration이 지나치게 많아지게 된다. 키우면 된다.

보통 3배씩 키워가거나 줄여가면서 변화시킨다고 한다.

또한 동작하는 가장 큰 rate를 찾은 후 그것보다 약간 작은 값을 최종적으로 사용한다고 한다.

- Feature의 설정과 polynomial regression

feature를 재정의하는 것도 하나의 좋은 방법이다.

예를 들어, 가로 넓이와 세로 넓이를 둘 다 feature로 사용하는 것보다 둘을 곱하여 면적이라는 새로운 feature로 정의하여 사용해도 문제가 없다. 

또한 polynomial regression이라는 방법도 있다. 

한 feature의 제곱이나 세제곱, 루트 등을 새로운 feature로 사용하는 방법이다. 

이러한 방법을 통해 위와 같이 선형에 적합하지 않은 데이터를 설명할 수 있다.

* polynomail regression도 '선형' 회귀이다. 모델 입장에서는 그냥 feature가 3개인 것이다. 

위 그래프를 보면서 어떻게 선형 모델인지 헷갈렸지만, 관점? 또는 차원의 문제로 이해할 수 있을 것 같다.

(https://stats.stackexchange.com/questions/92065/why-is-polynomial-regression-considered-a-special-case-of-multiple-linear-regres)

- Normal Equation

Normal Equation은 선형 회귀의 최적 파라미터를 찾는 또 다른 방법이다.

단 하나의 계산으로 해결되어 간단하지만 gradient discent와 각각 장단점이 있다. ㅇ

기본적으로 선형 회귀에서 cost function은 convex 하기 때문에 각 파라미터에 대해 편미분하여 0이 되는 값을 찾으면 최적 parameter를 찾을 수 있다. 

일일히 편미분하지 않고 그러한 값을 찾는 수식이 아래의 normal Equation이다.

X의 행과 열이 어떻게 구성되는지 주의해야 한다. (각 행이 1개의 데이터 셋으로 이뤄지고, 1이 맨 앞에 추가된다)

n은 feature의 수, m의 데이터셋의 수라고 할 때 X는 m x (n+1) 행렬이 된다. 

이때 X의 전치행렬과 X를 곱한 행렬을 A라고 하면 A는 (n+1) x (n+1) 의 정방 행렬이 된다.

어떤 행렬의 역행렬을 계산하는 것은 대략 O(n^3)의 시간 복잡도를 갖고, 따라서 feature가 많아질수록 이 과정에서 많은 시간이 소모될 수 있다.

*n >= 100,000 정도부터는 gradient discent를 고려하는 것이 좋고, 그 이상부터는 사실상 gradient discent를 사용한다고 한다.

결과적으로 (n+1) x 1의 결과가 나온다. n개의 feature에 대한 parameter가 계산된다. n+1인 이유는 intercept도 계산되기 때문이다.

자세한 수학적 증명은 우선 생략하였고, 또한 역행렬이 존재하지 않는 경우도 pseudo inverse 함수를 사용하면 해결이 가능하다 정도로 이해하고 넘어가면 될 것 같다.