AI

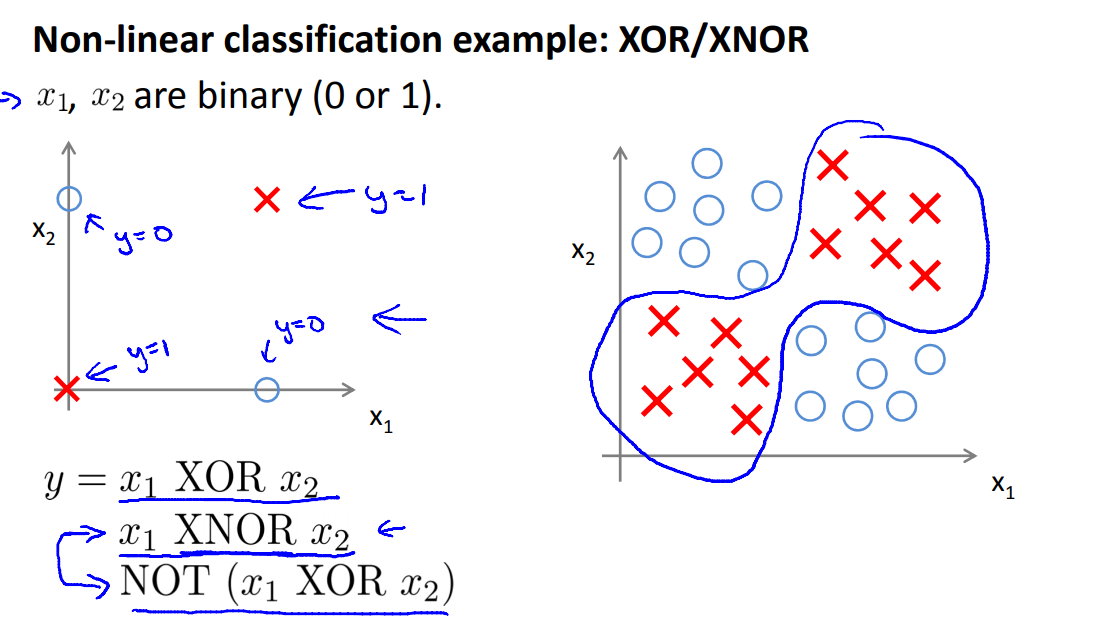
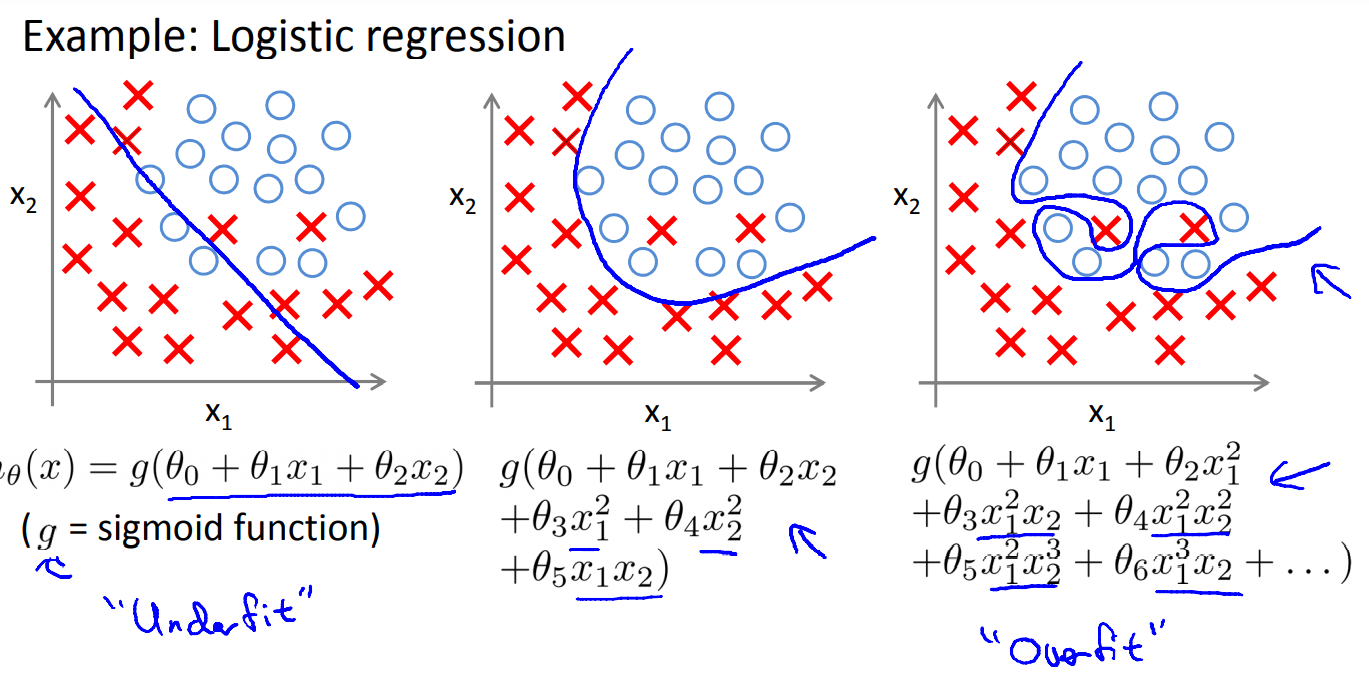
※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.

<성능과 diagnostic>

만약 학습시킨 모델이 새로운 데이터에 대해서 좋지 못한 성능을 보인다면 어떻게 해야할까?

위의 리스트와 같은 것들을 시도해볼 수 있을 것이다.

그러나 위 방법이 모든 경우에 성능을 향상 시키는 것은 아니고, 따라서 무작위하게 여러 방법들을 시도해보는 것은 비효율적이고 시간을 무의미하게 낭비할 가능성을 높인다.

따라서 적절한 diagnostic 을 이용해야한다.

한국말로 처방이란 뜻을 가진 단어답게, 현재 모델이 어떤 문제를 갖고 있고 어떠한 개선이 필요할지 확인하는 테스트이다.

<성능 평가와 Model Selection>

모델의 성능을 평가할 때는 training 데이터에 사용된 데이터로 계산된 cost function이 낮은 것만이 중요한게 아니라, 모델이 보지 못했던 데이터에 대한 예측력도 중요하다.

특정 데이터를 기준으로만 성능을 높이는 것을 over fitting을 유발하고, generalized 성능을 낮추기 때문이다.

따라서 주어진 데이터를 트레이닝에 사용될 데이터와 test에 사용될 데이터로 나누는 것이 일반적이다.(보통 7:3비율)

그러나 단순히 train/test set으로 나누게 되면 다시 test set으로 사용된 데이터를 기준으로 적합된 모델을 만들게 될 가능성이 크다.

그러한 문제를 막기 위해 train/cross validation/test 데이터셋으로 나누는 것이 좋다.(보통 6:2:2)

모델은 training data set을 이용해 학습시키고, cross validation data set을 이용하여 모델의 성능을 확인한 후, 마지막으로 test 데이터셋을 통해 최종적인 일반화 성능을 확인할 수 있다.

예를 들어, 위와 같은 경우에서 몇차항까지 feature로 사용해야 좋은 모델을 만들 수 있을지 결정하기 위한 과정은 다음과 같다.

1. 우선 training 데이터를 기준으로만 성능을 평가한다면 과적합을 방지할 수 없기때문에, train/validation/test data set으로 구분한다.

2. training data set을 이용하여 각 모델별로 파라미터를 학습시킨다.

3. 그렇게 학습된 모델별로 validation set에 대한 성능을 평가하고, 가장 좋은 성능을 보이는 모델을 선택한다.

4. 마지막으로 test data set을 통해 generalization error를 평가할 수 있다.

* 일반적으로 데이터가 충분하고 random하게 잘 구분지었다면, validation set에 대한 성능이 좋은 모델이 test set에 대한 성능도 좋게 된다.

* 성능 평가를 위해 사용하는 cost function에서는 regularization에 대해서는 고려하지 않는다. (즉 h와 y만 이용)

<Bias와 Variance 평가>

- Bias와 Variance

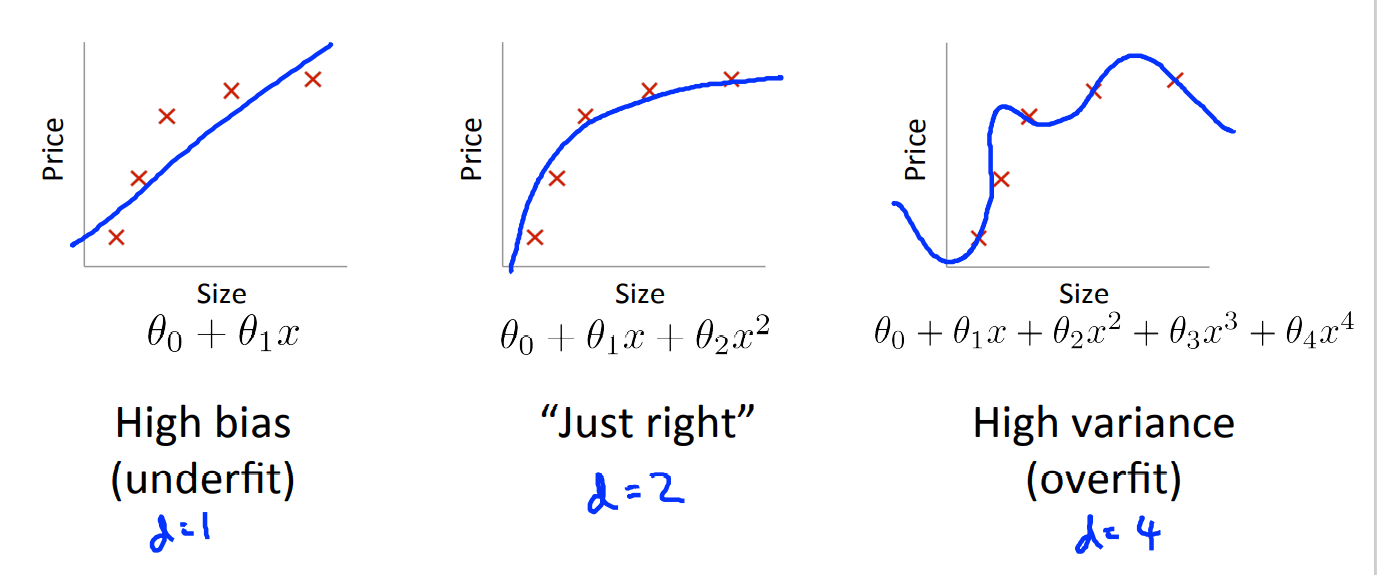
우선 Bias와 Variance의 의미는 다음과 같다.

High Bias : underfitting

High Variance : overfitting

(물론 별도의 수식이 있다.)

위의 그래프에서 빨간선은 training 데이터 셋에 대한 cost J 이고, 초록색은 CV data set에 대한 cost J이다.

(cost가 낮을 수록 좋은 예측 성능을 의미)

다항식의 차수를 추가할 수록, training set에 대한 설명력은 좋아지기 때문에(overfitting) 그에 대한 cost는 낮아진다.

반면 cv에 대한 cost는 차수가 낮을 때는 training과 동일하게 높다가(underfitting), 어느 정도 낮아진 후 과적합이 될수록 다시 향상되는 것을 확인할 수 있다.

다시 말해,

high bais인 경우, underfitting인 경우는 training data set과 cv data set 모두에 대해 예측 성능이 좋지 못하고,

high variance인 경우, overftting인 경우에는 training data set에 대한 성능은 좋지만 cv data set에 대한 성능은 좋지 못하다.

<Regularization과 bias/variance>

앞서 regularization 자체가 overfitting을 막기 위해 고려했던 작업인만큼 bias, variance 문제에서 중요하다.

위 그림과 같이 하나의 모델에서도 regularization parameter 람다를 크게하냐 작게하냐에 따라 overfitting과 underfitting 문제가 발생할 수 있다. 반대로 적당하게 조정하여 문제를 해결할 수도 있다.

- regularization parameter 선택

그렇다면 어떻게 적당한 크기의 람다를 선택해야될까? 단순히 앞에 정리했던 내용을 바탕으로 선택하면 된다.

여러 값의 람다에 대해 트레이닝시킨 모델들을 만들고, cv data set을 통해 성능을 확인해보고 가장 좋은 모델을 선택하면 된다. 이 후 test data set을 통해 일반화 성능도 확인할 수 있다.

 람다를 x축, cost를 y축으로 놓고 그래프를 그리면 일반적으로 위와 같이 그려질 것이다. 

<Learning Curves>

bias와 variance가 높은 경우 각각 traning에 데이터가 많아질수록 모델의 정확도가 변화하는 양상이 다르다.

- bias가 높은 경우

(1) training 데이터가 많아질수록 train error는 커진다. 

(2) cv 셋에서 대한 error는 데이터가 많을 수록 작아진다.

(3) 그러나 둘 다 점진적으로 plat한 형태가 되고 결국 매우 비슷하게 된다. 이때의 error는 큰 값으로 볼 수 있다.(underfit 되어 있기 때문에)

- high variance 인 경우

(1) m이 커질 수록 train에 대한 오류가 커지긴 하지만 크지 않다.(overfitting)

(2) cv data set에 대한 오류는 m이 커질수록 작아지지만, train에 대한 오류에 비하면 큰 gap을 갖는다.

(3) m이 커질수록 그 gap은 작아진다. 

위 두 내용을 통해 알 수 있는 점은 다음과 같다.

high bias 문제라면 데이터를 늘리는 것이 도움이 되지 않을 가능성이 크고,

high variance 문제라면 데이터를 늘리는 것이 도움될 가능성이 크다.

이러한 점을 알면 가장 처음에 말한 무의미한 시도를 줄일 수 있다.

<정리>

그렇다면 초반에 말한 해결책들이 어떤 경우에 쓰일 수 있는지 다시 보자.

어렵지 않게 이해할 수 있다.

< Neural Network의 경우? >

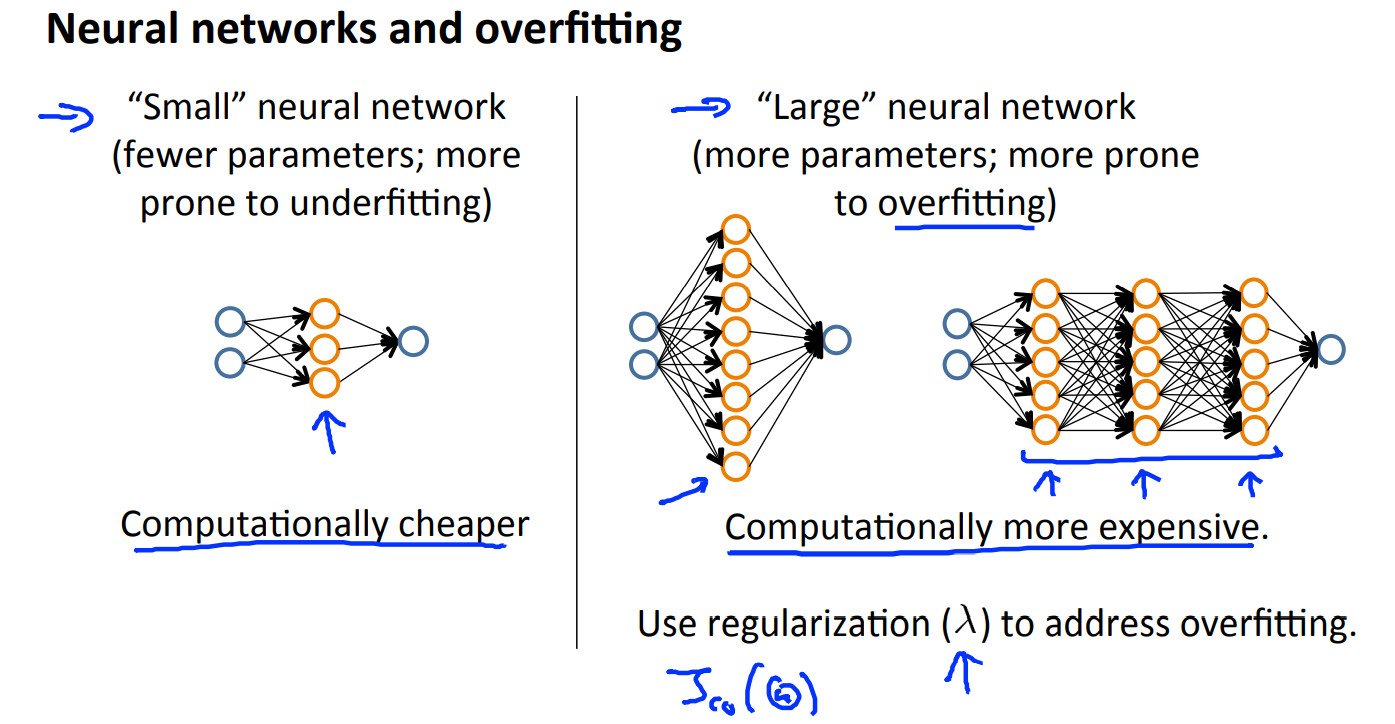
이번 강의에서 다룬 내용과, 뉴럴 네트워크에서 hidden layer가 새로운 변수를 만드는 것과 유사하다는 점을 고려하면 아래 내용 또한 자연스럽게 이해할 수 있다.

우선 NN 자체가 너무 작다면 underfitting에 취약하다. 직관적으로도 이해할 수 있고, parameter가 적으니 underfitting 될 가능성이 큰게 당연하다.

반대로 NN의 netwrok가 크다면 overfitting에 취약하다. 같은 원리로 이해할 수 있다.

따라서 Neural Netwrok에서는 다음과 같은 조치를 취할 수 있다.

(1) 다항식의 차수를 변화시켜가며 model selection을 했던 것을 hidden layer의 계층의 수를 변화시켜가며 동일하게 적용해볼 수 있다.

(2) regularization parameter를 조정하여 overfitting을 해결한다. 

※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.

- Cost Function

Nueral Network에서의 cost function은 다음과 같다.

비교적 복잡해보일 수 있지만 크게 다른 내용은 없다. 

좌측의 2개의 sum에서 i는 input에 대해, k는 class에 대해 대응된다. 즉, input 별로 실제값과 예측값의 차이를 합하는 식이다.

우측의 3개의 sum으로  구성된 식은 단순히 모든 계층의 theta 값의 합이다.(for regularization)

- Backpropagation Algorithm

Neural Network에서 output은 input으로 입력된 값부터 layer를 순서대로 거치며 forwardpropagation 과정을 통해 연쇄적으로 계산된다.

$ z^{(l)} = \Theta ^{(l-1)}a^{(l-1)}, a^{(l)} = g(z^{(l)}) $

반대의 순서로 이뤄지는 Backpropagation을 통해 다음의 값을 계산할 수 있다.

gradient discent 등의 최적화 알고리즘을 적용하기 위해 cost function과 각 파라미터에 대한 편미분 값이 필요한데, cost function의 식은 앞서 살펴보았고 편미분 값을 Backpropagation을 통해 찾을 수 있다.

자세한 과정은 다음과 같다.

- for one input

$ \delta {_{j}}^{l} $는 l번째 계층에서 j번째 unit의 error를 의미한다. 

우선 L번째 layer(output layer, 여기서는 4번째)에서는 예측값-실제값을 계산하여 $ \delta$를 계산할 수 있다.

이 후의 layer에서는 

$ \delta^{(l)} = (\Theta^{(l)})^{T}\delta ^{(l+1)}.*g'(z^{(l)}), $   $ g'(z^{(3)}) = a^{(l)}.*(1-a^{(l)}) $

의 식으로 계산한다. g'과 a(1-a)는 미분과정을 통해 증명이 가능하다고 한다.(생략) 

이 전 layer(더 output 에 가까운) 의 델타값을 통해 연쇄적으로 계산되는 것을 알 수 있다.

참고로 (1)번째 layer는 input layer 이므로 계산할 오류가 없다. 

또한 regularization을 무시한다면 다음과 같은 식 또한 성립한다.(증명 생략)

$ \frac{\partial }{\partial \Theta {_{ij}}^{l}}J(\Theta ) = a{_{j}}^{(l)}\delta {_{i}}^{(l+1)} $

이처럼 Backpropagtion을 통해 계산한 delta를 통해 파라미터의 편미분 값을 계산할 수 있다. 

- 여러 개의 input

위는 하나의 input에 대해 계산 과정을 나타낸 것이고, 모든 input에 대해서는 

\Delta {_{ij}}^{(l)}

를 이용하여 누적값을 계산한다. 위 식은 (l)번째 layer의 i행 j열 parameter에 대한 누적 값을 의미한다.

대문자 Delta 를 0으로 설정해놓고 input = 1~m까지에 대해 propagtion과 delta를 각각 계산한 후

$ a{_{j}}^{(l)}\delta {_{i}}^{(l+1)} $

위 값을 누적으로 더하는 방식으로 계산하면 된다.

마지막으로 m으로 나누고 regularization을 적용하여(람다*paramter의 값) D를 계산하면, 

D가 cost function을 각 paramter로 나눈 편미분 값을 계산한 matrix가 된다.

* input 이 i = 1~m 으로 표현되어 있어 헷갈렸는데, 대문자 Delta와 D에서의 ij는 i행 j열을 의미한다. 

- Unrolling parameter

fminunc와 같은 방법을 이용하여 최적 세타를 계산하려면 initial theta나 gradient값을 계산한 것이 vector 가 되어야 한다. 그러나 NN에서는 vector가 아니라 각 계층 별 matrix 형태인 문제가 있다.

따라서 위 코드에 적용하기 위해서는 unrolling을 해야하는데, 이론적으로 특별한 내용은 없고 그냥 다음과 같이 적용하면 된다. 

unrolling하여 전달한 후, 다시 reshape하여 계산하고, 계산한 값을 다시 unrolling하여 vector로 반환하면 된다.

* Octave기준 unrolling은 'vector(:)' 문법을 통해, reshape는 reshape((start:end), row, column) 문법으로 구현한다.

- Gradient Checking

NN에서 backpropagation을 계산하는 과정에서 잘못된 설정, bug들이 포함되어도 언뜻 문제없이 계산되는 것처럼 보이는 경우들이 있다. 

gradient checking을 계산이 의도한 대로 이뤄지고 있는지(편미분값이 정상적인지) 확인하는 하나의 방법이다.

반드시 적용해보는 것이 좋다.

방법은 그렇게 복잡하지 않다.

미분의 개념을 바탕으로 실제 미분값을 근사적으로 계산해본 후 backpropagation으로 계산한 값과 비교해보면 된다.

입실론은 작을 수록 좋지만, 프로그램 계산 상의 이유로 10^-4 정도로 설정한다. 

편미분으로 확장하면, theta를 unroll 한다음 적용하면 된다. 

단, 위 계산이 backpropagtion에 비해 훨씬 오래 걸리기 때문에 한번 검사를 마친 후에는 disable 해야한다. 

ex) gradient discent를 적용할때마다 비교 -> very slow

- Random Initialization

앞서 logistic regression 등에서는 gradient discent 등을 적용하기 전 초기 파라미터를 0으로 설정했었지만,

NN에서는 초기 파라미터를 0으로 설정하거나 하나의 값 통일된 값으로 설정하면 안된다.

(* 기본적으로, NN에서 cost function은 convex하지 않다. -> 파라미터를 아무값이나 해도 global optimum을 찾지 않는다.)

0 또는 하나의 통일된 값으로 설정하면 안되는 이유는 다음과 같다.

1. 가장 처음 계산에서 모든 파라미터가 같다면 같은 layer에서 모든 unit의 output이 동일하게 된다.

마찬가지로 backpropagation에서도 같은 layer의 unit끼리 모두 같은 delta값을 갖게 되고, 

2. 결과정으로 같은 layer의 편미분값이 동일하게 된다. 즉, 최적화 과정에서(gradient discent) 파라미터의 증가 또는 감소가 동일한 값으로 이뤄지고, 파라미터는 계속하여 같은 값이 유지된다.

3. 모든 layer에서의 output이 같다는 것은 사실상 layer마다 하나의 unit 밖에 없는 것과 동일하고, 이는 처음 설계했던 Network의 구조를 의미없게 만드는 것이다. 

해결 : random initialization: Symmetry breaking

위와 같은 문제를 해결하는 것을 symmetry breaking이라고 하고, random initailization으로 해결한다.

-입실론 ~ 입실론 범위의 rand한 value로 초기화하는 방식을 선택하면 된다. 구현 코드는 위와 같다.

여기서의 입실론도 0에 가까운 작은 수를 택하면 된다.(gradient checking과는 다른 입실론)

- Neural Network 구조 설정

hidden layer는 1개 이상이며 각 hidden layer끼리는 unit수를 통일하는 것이 일반적이다. 

자세한 내용은 이후의 강의에서 다룸.

- Non- Convex

앞서 잠깐 얘기했듯이 NN에서 cost function은 convex하지 않다.

그러나 실질적으로는 local minimum을 찾더라도 상당히 좋고, 큰 문제가 되지 않는다고 한다. 

(local minimum과 global minimum의 차이가 미미한듯) 

※ 본 내용은 Coursera, Machine Learning - Andrew Ng 강의, 강의자료를 바탕으로 작성하였습니다.

<Neural Network>

- Non-linear classification

데이터를 항상 linear한 모델로는 설명할 수 없다.

이를 해결하기 위해 앞서 polynomial regression과 같은 방법을 이용하여 non-linear한 classfication을 수행하였다.

그러나 이러한 방식으로는 n개의 feature를 통해 대략 이차항의 조합만 추가하여도, $ \frac{n^{2}}{2}$개에 비례하는 새로운 feature를 만들게 된다.

3차항 이상의 조합까지 추가하면 feature의 수가 굉장히 많아져, 연산이 사실상 불가능하거나 지나치게 오래걸리게 된다. 

또한 이미지 처리의 경우 각 pixel 위치마다 feature로 처리하면,

간단하게 50x50 크기의 이미지만 처리하려해도 1차항으로 2500개의 feature가 나온다.(gray scale)

여기에 이차항 조합까지만 추가하려 해도 3 million 개의 feature가 나오게 된다.

- Neural Networks

따라서 Neural Network는 이러한 문제를 해결할 수 있는 non-linear 모델으로, 

실제 뇌의 뉴런 세포들의 동작을 mimic 하는 방식으로 학습하는 알고리즘이다. 

- 뉴럴 네트워크 구조

layer구조를 이루어, input layer와 output layer 그리고 그 사이의 hidden layers로 구성되어 있다. 

- input layer와 output layer는 이름 그대로 입력과 출력값을 의미하고, 그 외의 layer를 모두 hidden layer라고 한다.

- 노란색으로 표시된 unit 들이 하나의 뉴런에 대응된다고 보면 된다. 

각 뉴런에서 하는 일은 logisitic regression에서 하는 일과 동일하다. 즉 sigmoid function의 값을 계산하는데, 뉴럴 네트워크에서는 activation이라고 표현한다. 위 그림에서 $ a$로 표현된다. 

* $ a_{i}^{(j)} $는 j layer에서 i번째 unit의 activation을 의미한다. 

* bias unit은 항상 1의 값을 갖는 값으로, 계층의 0번째 activation으로 보면 된다. 그림에서는 생략하는 경우가 많다.

- 내부 동작(계산)

각 activation의 계산 과정을 자세히 살펴보면 다음과 같다.

* $ \Theta^{j} $는 matrix of weights를 의미한다. (뉴럴 네트워크에서 각 파라미터를 weights, 가중치로 표현한다.)

파라미터의 결정에 대해서는 이후에 다룬다고 한다.

어쨌든 위 식을 계산하려면, 슬라이드의 밑에 나와있는 것처럼 $ \Theta $는 $s_{j+1} \times (s{_j}+1) $ 크기의 matrix가 된다. +1은 bais unit에 의한 것이다.

식이 조금 복잡하기 때문에 다음과 z를 다음과 같이 정의하여 나타낼 수도 있다.

$ z{_{k}}^{j} = \Theta {_{k,0}}^{(j-1)}x{_0} + \Theta {_{k,1}}^{(j-1)}x{_1} + ... + \Theta {_{k,n}}^{(j-1)}x{_n}, $

vectorization을 적용하면 다음과 같다. input layer는 $ a^{(1)} $으로 취급하면 된다.

$ z^{j} = \Theta ^{j-1}a^{j-1} $ 

최종적으로 

$ a^{j} = g(z^{(j)}) $

와 같이 나타낼 수 있다. 

- 장점

위 그림과 같이 input layer를 가려본다면, layer 2를 input layer로 봐도 문제가 없다.

즉,  Neural Network 구조에서는 임의로 feature를 생성하지 않아도,

계속해서 새로운 feature를 learning한다고 볼 수 있다. 

- Simple Example

간단한 non-linear classification의 적용 예시는 다음과 같다.

위와 같은 데이터를 분류하기 위해선, non-linear한 모델이 필요한 것을 알 수 있다.

참고로 x1 XNOR x2 연산을 통해 분류할 수 있다. 

우선 AND 로직은 위와 같이 가중치를 설정하여 계산할 수 있다. truth table을 통해 쉽게 이해할 수 있다.

최종적으로 위와 같은 구조를 통해 XNOR을 구현할 수 있다. 

(OR 등의 로직도 truth table을 통해 간단히 확인할 수 있으므로 생략)

이번 예시는 간단한 예시이지만, 이를 통해 

뉴럴 네트워크의 구조를 잘 설계하여 복잡한 로직의 처리도 가능하다는 것을 알 수 있다. 

- Multi-Class Classification

output layer의 unit을 1개가 아닌 여러개로 설저하고, output을 vector로 다루면 multi-class classification으로도 확장이 가능하다.

<Regularization>

- Regularization이란?

모델이 새로운 데이터를 접하더라도 좋은 예측 결과를 유지하도록 만드는 것.

즉, overfitting을 해결하는 것이다. 

overfitting이란 학습에 사용된 training 데이터에 지나치게 모델이 지나치게 적합되는 것으로, 

새로운 데이터에 대한 일반적 성능을 저하시킨다. (high variance)

linear regression과 logistic regression 두 경우 모두 발생할 수 있으며, 각 경우를 시각화한 그림은 다음과 같다.

반대로 underfitting 또한 존재한다 (high bias). underffiting이 일반적 성능을 향상시키는 것은 아니다.

- Overfitting을 해결하는 방법

위 슬라이드처럼 1. 불필요한 feature를 줄이거나, 2. regularization 기법을 사용하면 된다.

방법 1의 경우 유의미한 데이터를 버리게 될 수도 있고, 임의로 feature를 선택하기 어려울 수 있다.

(후에 selection 알고리즘을 다룬다고 한다.)

방법 2 regularization은 parameter의 magnitude를 줄인다고 나와있는데, 

이는 해당 특성이 모델의 결과값에 미치는 영향을 줄이는 것을 의미한다.

( 해당 특서에 대한 parameter 값이 작아지면 영향이 당연히 줄어든다. ) 

- Regularization, Cost Function

regularization을 설명한 슬라이드는 다음과 같다.

cost function에 파라미터를 포함시켜서 원하는 파라미터를 penalize 하는 방식으로 regularization을 구현하는 것을 확인할 수 있다.

cost function에서 파라미터 앞에 붙은 숫자 1000은 위 예시에서 임의로 붙인 숫자로, 일반적인 식에서는 람다로 표현한다. 일반적인 식은 다음과 같다. 

앞서 사용했던 cost function에 각 파라미터의 값을 추가하여 regularization을 구현한다.

보통 intercept를 제외한 모든 파라미터에 대해 하는 것이 일반적이다.

람다가 클수록 각 파라미터는 작아질 것이고, 

반대로 람다가 작다면 파라미터의 크기가 cost function에 미치는 영향이 작기 때문에 regularization이 잘 이뤄지지 않을 수 있다.

즉, fit-well 하는 것과 parameter를 줄이는 것(regularization) 는 trade-off 관계이며, 람다를 적절하게 설정해줘야 한다.

- Linear Regression Optimize (Gradient Discent, Normal Equation)

regularization을 고려하여 새로 정의된 cost function에서 최적 parameter를 찾는 과정도 동일하다.

(1) Gradient Discent

기본 알고리즘에서 cost function을 미분한 값만 변경하여 적용하면 된다.

그 결과 위와 같은 식으로 정리되고, 편미분 또한 어렵지 않게 할 수 있다.(생략)

주의할 점은 intercept parameter, j = 0인 경우는 regularization을 적용하지 않는다는 점이다.

(2) Normal Equation

결과적으로 Noraml Equation 수식은 다음처럼 바뀐다. 

기존의 Normal Equation이 각 파라미터에 대해 편미분한 값이 0이 되는 값을 찾는 것과 동일한 것처럼,

위 식도 같은 과정으로 유도된다고 한다.(생략)

참고로, m < n인 경우 $ X^{T}X $가 singular 하지만, 위 식을 적용하면 invertible 하다고 한다.(증명 생략)

즉, pinv가 아닌 inv만 제공하는 라이브러리 만으로도 적용할 수 있다. 

- Regularized Logistic Regression

Logistic Regression도 regularization이 필요하다. 

기본적인 원리는 동일하고, 수식만 logistic regressionn에 맞춰 적용하면 된다.

cost function

마찬가지로 기존 식에 파라미터의 값이 더해진다. 

Gradient Discent

위의 cost function을 편미분한 식만 달라진다. 편미분 과정 또한 어렵지 않다.(생략)

마찬가지로 j=0인 경우는 regularization을 수행하지 않는다.