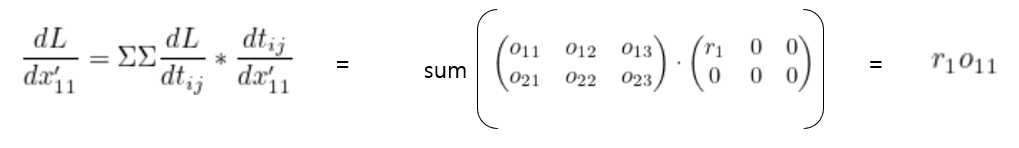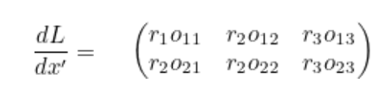AI

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 11에서는 detection과 segmentation에 대해 다루고 있다. 

앞선 강의에서 classification에 대해 중점적으로 다뤘지만, 위에 소개된 detection이나 segmentation도 computer vision 분야의 핵심적인 tasks이다. 

Sematic segmentation부터 instance segmentation까지 각가의 task와 관련 기술에 대해 살펴보겠다.

<Semantic Segmentation>

Semantic segmantation은 이미지 내의 모든 pixel에 대해 어떠한 class에 속하는지 labeling을 수행하는 task이다.

Instance segmentation이나 detection과의 가장 큰 차이 점은 각각의 객체를 구분하지 않는다는 것이다. 

그 예시로 위 슬라이드에서 두 마리의 소를 구분짓고 있지 않다. 

그렇다면 semantic segmentation은 어떻게 수행할 수 있을까?

- Sliding Window?

가장 먼저 window 크기만큼 이미지의 일부 영역에 classification을 수행하고, window를 이동시켜가며 이미지의 각 영역에 대해 classification을 수행하는 방법을 생각할 수 있다.

그러나 영역을 구분짓기 위해서는 window size가 크지 않을 것이고, 따라서 계산이 상당히 많이 필요하다는 것을 쉽게 예상할 수 있다. 

- Fully Convolutional

Fully connected layer 등을 제외하고, 최종 출력까지 conv 연산의 결과가 되도록 모델을 설계하는 방법도 존재한다.

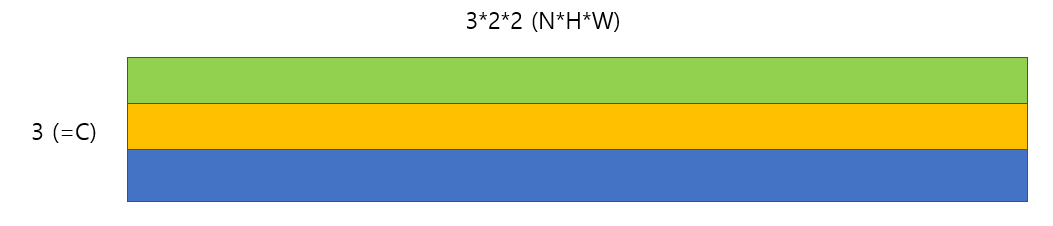
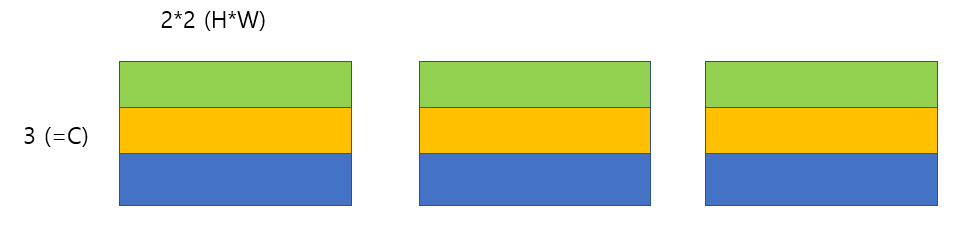
최종 출력은 CxHxW 크기가 될 것이고(C : # of category), 최종 output에서 각 pixel별로 score를 확인하여 classification을 수행하면 된다.

좋은 방법이지만 마찬가지로 high resolution image을 유지하기 위해서는 계산량이 상당히 많아지게 된다. 

예를 들어 226x226 크기의 이미지가 주어지면 최종 출력도 226x226 크기가 돼야하므로 conv연산을 거치는 과정에서 연산이 상당히 많이 필요할 것이다. 

이러한 문제는 downsampling과 upsampling을 어느 정도 극복할 수 있다.

Maxpooling 등의 방법으로 downsampling을 거쳐 데이터의 크기를 줄여서 처리한 후, 다시 upsampling을 겨쳐 원본 이미지의 크기에 맞춰 출력하는 방식이다. 

Pooling과 반대되는 unpooling을 통해 upsampling을 수행할 수 있고, 위와 같은 방법들을 생각해볼 수 있다.

또한 umsampling 과정 또한 학습이 가능한 방법인 'Transpose Convolution'도 존재한다. 

Transpose convolution은 input의 각 element를 filter에 곱해서(broadcasting) output을 출력하는 방법이다. 

1차원 예시로 다시 한 번 나타내면 다음과 같다.

해당 과정이 'Transpose Convolution'이라고 불리는 이유는 다음과 같다.

기본적으로 모든 convolution 연산은 좌측과 같이 행렬곱으로 나타낼 수 있고, 해당 연산을 transpose하면 transpose convolution이 된다. 

따라서 'Tranpose Convolution'이라는 이름을 사용하고,

그 외에 Deconvolution, Upconvolution 등의 명칭으로 불리기도 한다. 

겹치는 영역에 대해서 평균을 취하지 않고 더하는 이유에 대해 질문이 있었는데, filter가 slide하며 겹치는 영역의 결과를 더하는 이유도 위 연산 과정을 따르기 때문이다.

실제로 scale이 달라지는 등의 문제가 존재하긴 하고, 다양한 방법으로 해결하려는 연구가 존재한다고 한다.

<Localization>

Localization은 classification뿐만 아니라 실제 그 객체가 위치한 영역을 탐지까지 하는 task를 의미한다. 

단, detection과 달리 단 하나의 객체만을 탐지한다.

Localization은 classification과 유사하게 수행하고, 박스의 좌표에 대한 vector를 출력에 추가해서 regression처럼 다루는 방식으로 수행할 수 있다. 

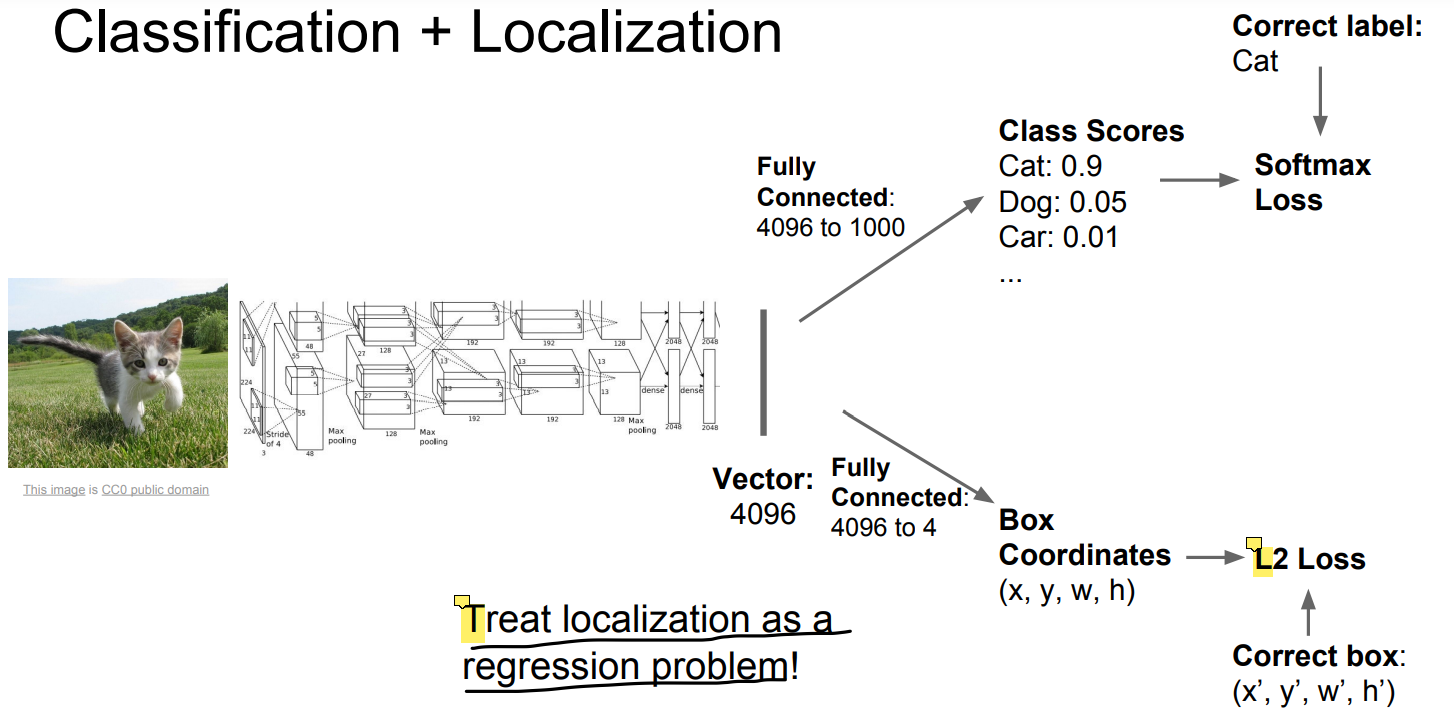
위와 같은 방법을 사용하면 (1) classification에 대한 loss, (2) regression에 대한 loss, 총 2가지의 loss가 존재하게 된다.

보통 이러한 경우 각 loss에 weight를 주어서 a*Loss1 + b*Loss2 등과 같이 하나의 loss로 통합해준다.

이때의 weight 또한 hyperparameters이지만, 설정에 따라 loss 자체가 달라지기 때문에 일반적인 hyperparameter와 달리 loss가 낮아지는 방향으로 선택하는 것이 어렵다.

따라서 loss외에 다른 지표를 하나두고, 해당 지표를 바탕으로 어떠한 weight 설정이 좋을 것인지 판단하는 방법을 사용하기도 한다.

※ Accuracy 등이 있을 것 같다.

또한 같은 convolution 구조를 이용하면서 fully connected layer만 fine tuning하는 방식으로 2개의 모델을 생성한 후,

각각 classification과 loss를 계산하도록 구현하는 방법에 대한 질문이 있었다.

가능한 방법이지만, 둘을 통합할 때 문제가 발생할 수 있으므로 가능한 하나의 모델로 수행하는 것이 좋다고 한다.

+ Pose Estimation

Regression을 접목하는 방식은 다양한 task로 확장이 가능하고, 대표적으로 아래와 같이 사람의 관절 위치를 탐지하는 것도 가능하다.

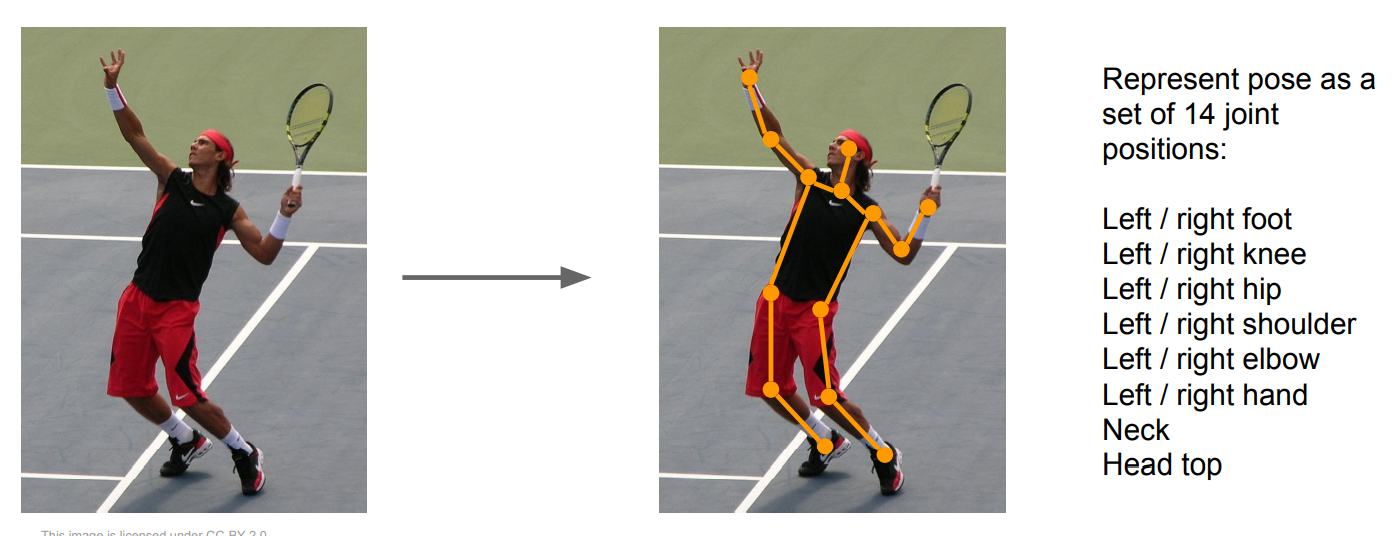
Localization에서 박스의 좌표를 다룬 것처럼, 각 관절 좌표에 대한 regression을 수행하도록 구현할 수 있다.

<Object Detectoin>

Object detection은 여러 개의 객체를 탐지하는 task이며, classification처럼 deep learning의 등장 이 후 크게 발전한 분야이다.

앞서 다룬 Localization과의 차이점은 여러 개의 객체를 탐지한다는 것이며, 따라서 객체의 수가 고정되어 있지 않으므로 Localization과 같이 구현할 수 없다.(Output의 수가 고정되어 있지 않으므로)

- Sliding Window?

가장 먼저 sliding window를 떠올려 볼 수 있지만, semantic segmentation에서와 마찬가지로 연산의 수가 매우 많아질 것이다.

- R-CNN, Region Proposals

R-CNN은 Region Proposal을 이용한다.

Region Proposals는 전통적인 image processing 알고리즘으로, 이미지 속에서 object를 포함할만한 영역을 표시해준다.

제안되는 영역이 많고 정확하지는 않아서 해당 방법만으로 detection은 불가능하고, 제안되는 영역에 대해서만 classification을 수행한다.

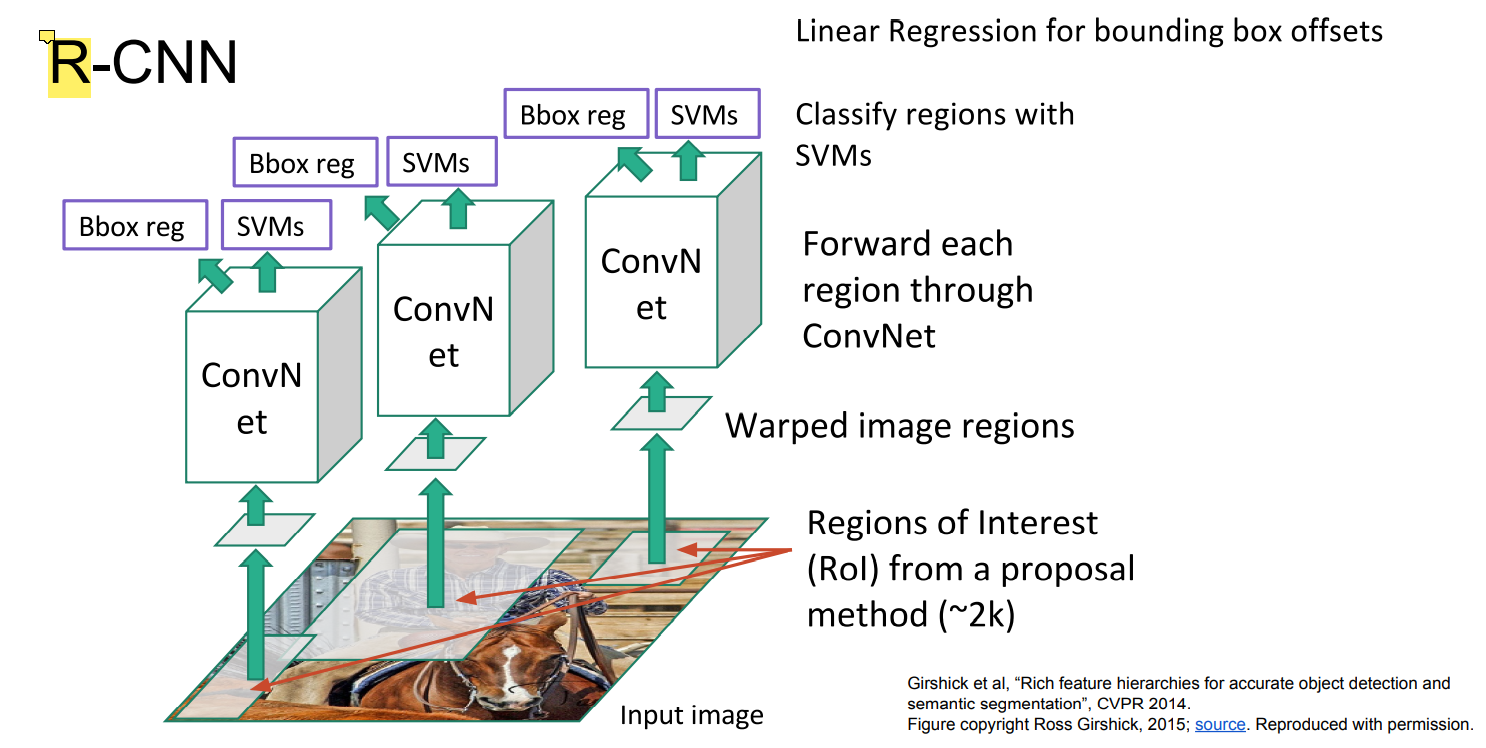
여기에서도  

 (1) classification에 대한 loss

 (2) 제안된 영역의 적합성에 대한 loss

총 2가지 loss가 존재한다.

R-CNN은 그림에서 볼 수 있듯이 여러 번 연산을 수행하므로, 여전히 비효율적인 방법이다.

- Fast R-CNN

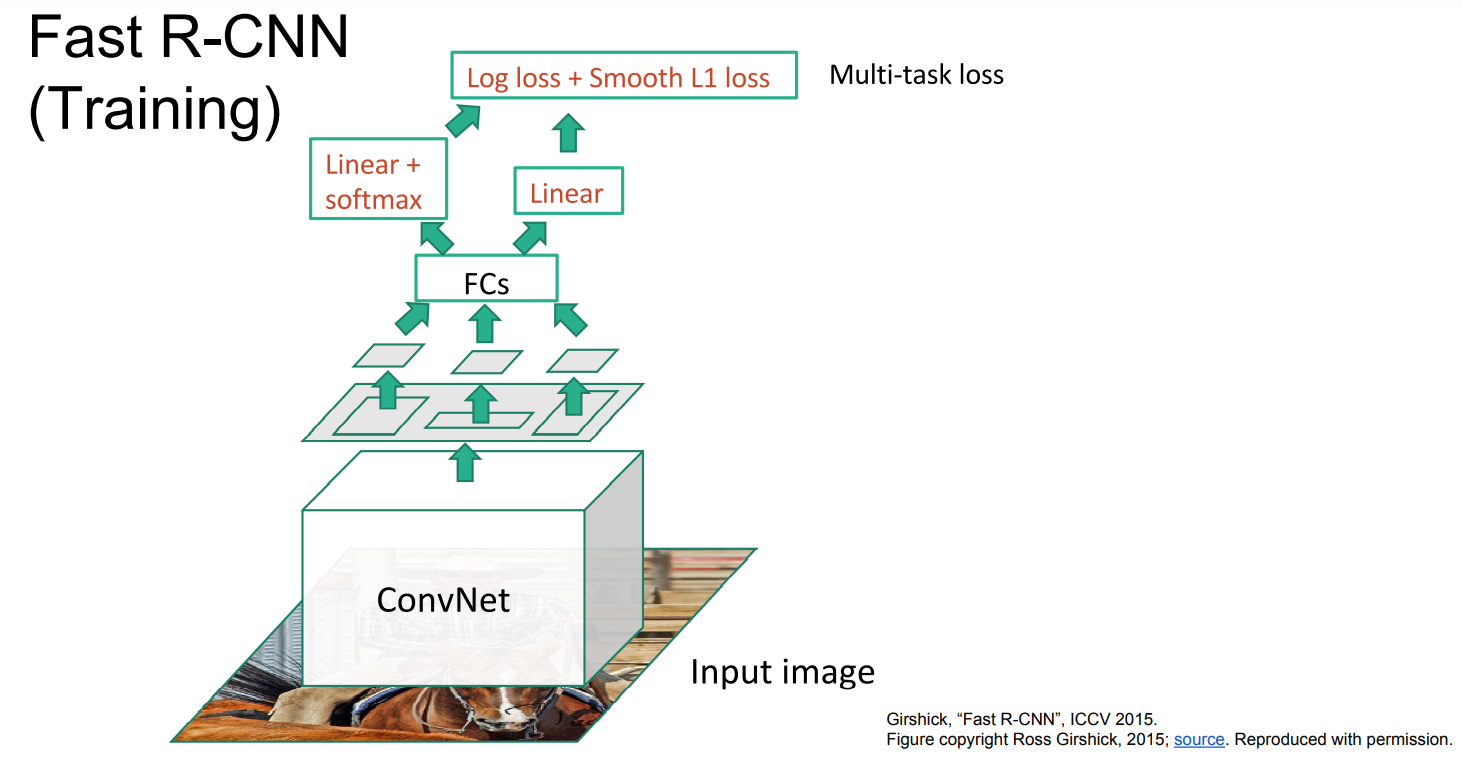
Fast R-CNN에서는 먼저 하나의 Convoultion network를 거친 결과에 대해서 region proposal 결과를 이용하는 방법이다.

그림에서는 작아지는 것으로 표현되었지만, ConvNet을 거친 후의 size(HxW)는 input image와 동일하고, input image로 생성된 region proposal 영역을 ConvNet을 거친 결과에 적용하는 것이다.

이 후에는 각 영역에 대해 FC layers를 이용해 classification을 수행한다.

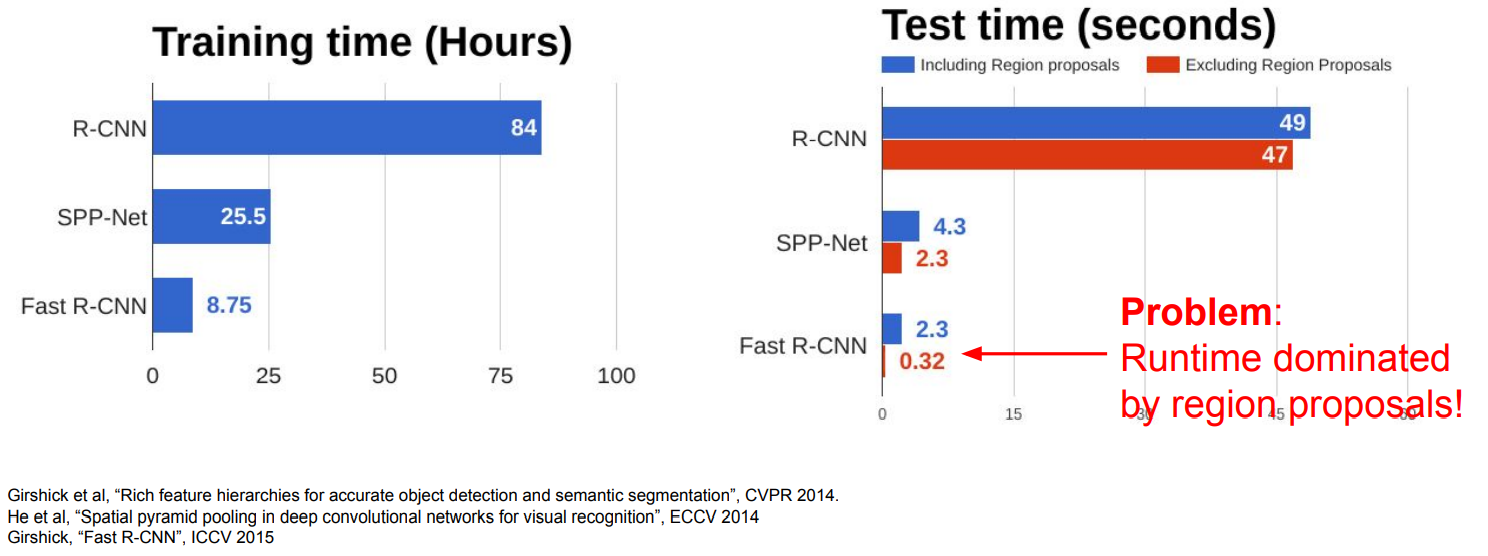
Fast R-CNN은 R-CNN에 비해 훨씬 빠르지만, runtime이 region proposals 알고리즘의 계산 시간에 의해 결정된다는 단점이 존재한다.

(SPP는 R-CNN과 Fast R-CNN의 중간 정도의 방법이라고 한다.)

따라서 최종적으로 Faster R-CNN을 통해 그러한 문제도 극복한다.

- Faster R-CNN

Faster R-CNN에서는 region proposal도 deep learning으로 처리한다. 

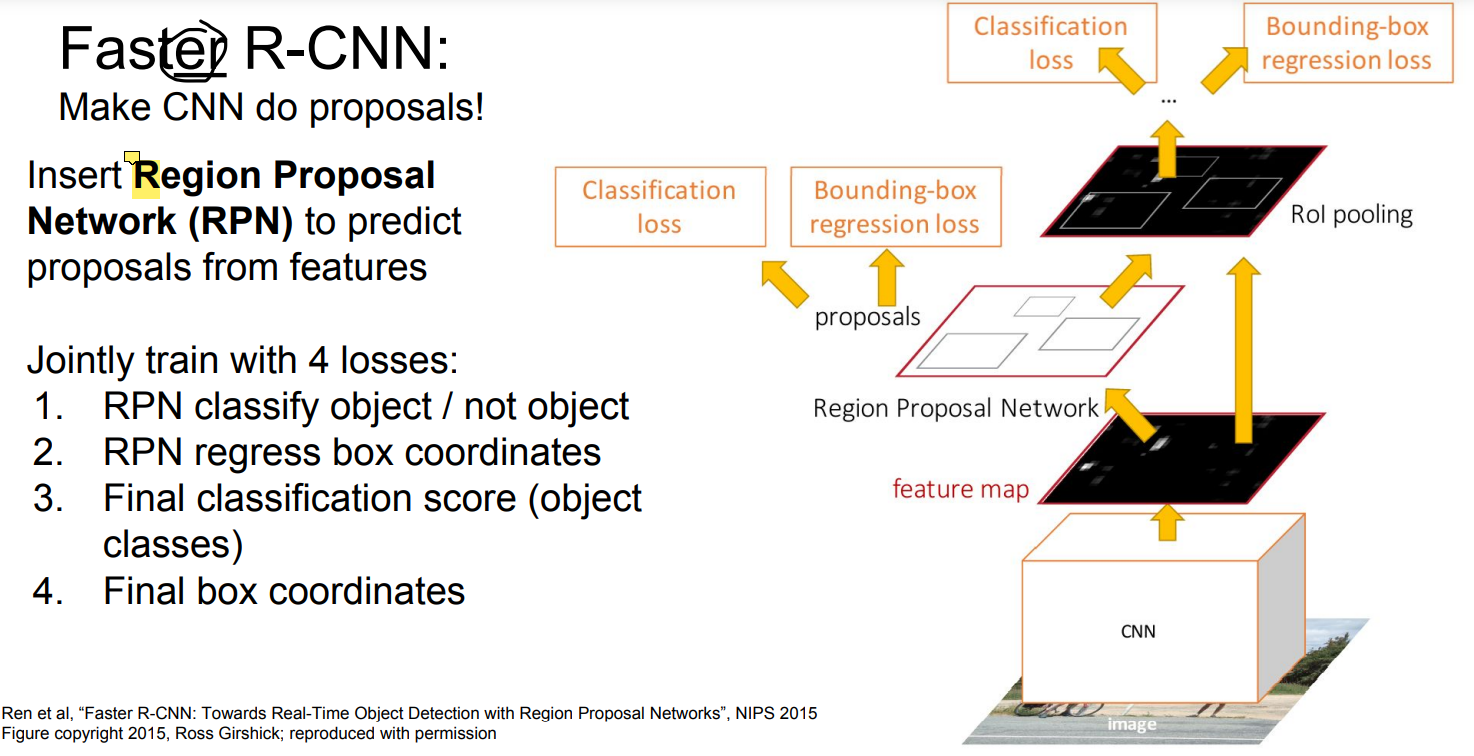
RPN(Region Proposal Network)를 추가하여 region proposal이 오래 걸리던 문제를 해결하는 것을 제외하고는 Fast R-CNN과 동일하다.

Regision proposal에 대한 loss가 2개 추가되어 총 4가지 loss가 존재하게 된다. 

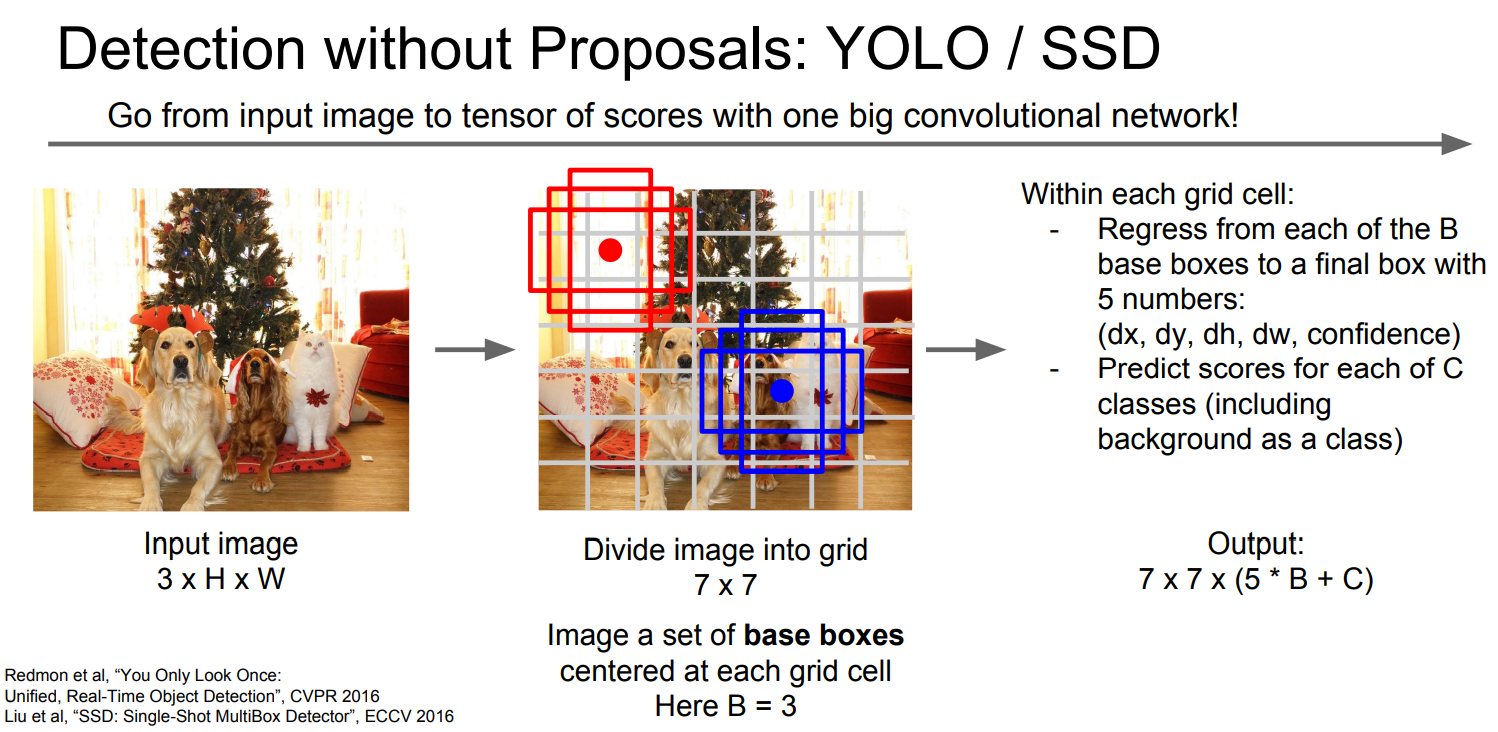
그 외에 YOLO나 SSD같은 방법도 존재한다고 한다.

이미지를 grid단위로 나누고 -> grid 마다 모든 base box 경우에 대해  <dx, dx, dh, dw, confident>를 예측

-> classification을 수행

위와 같은 순서로 동작한다고 한다.  

<Segmentation>

Multiple objects를 탐지하고, pixel 단위로 segmentation을 수행하는 task이다.

앞서 다룬 semantic segmentation과 detection을 결합하여 구현할 수 있다. 

Object detection을 먼저 수행하고, 제안되는 bounding boxes마다 sematic segmention을 수행하는 방법이라고 생각할 수 있다. 

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Assignment2 - Q4에서는 convolution layer, pooling layer를 구현하고, 최종적으로 CNN을 구현한다.

추가로 CNN에 특화된 batch normalization layer인  spatial batch normalization layer을 구현하는 내용 또한 다루고 있다.

그 중 convolution layer의 역전파 수식과 spatial batch normalization의 구현에 대해 정리해보겠다. 

<Convolution layer의 역전파>

Convolution layer의 역전파 또한 이전과 동일하게 chain rule을 이용해 계산할 수 있다. 

$ X = \begin{pmatrix}
x_{11}& x_{12} & x_{13}\\
x_{21}& x_{22} & x_{23}\\ 
x_{31}& x_{32} & x_{33}\\
\end{pmatrix},
W = \begin{pmatrix}
w_{11}& w_{12}\\
w_{21}& w_{22}\\
\end{pmatrix}, bias = b $,

간단하게 3x3 input과 하나의 2x2 filter 간의 convolution 연산을 살펴보겠다. (stride = 1, padding = 0)

위 예시만으로도 convolution 역전파 방식에 대해 파악할 수 있다. 

$Y = \begin{pmatrix}
x_{11}w_{11} +x_{12}w_{12} +x_{21}w_{21} +x_{22}w_{22} + b& x_{12}w_{11} +x_{13}w_{12} +x_{22}w_{21} +x_{23}w_{22} + b\\
x_{21}w_{11} +x_{22}w_{12} +x_{31}w_{21} +x_{32}w_{22} + b& x_{22}w_{11} +x_{23}w_{12} +x_{32}w_{21} +x_{33}w_{22} + b\\ 
\end{pmatrix} $

$ = \begin{pmatrix}
y_{11}& y_{12}\\
y_{21}& y_{22}\\
\end{pmatrix} $

$ dout = \begin{pmatrix}
\frac{dL}{dy_{11}}& \frac{dL}{dy_{12}}\\
\frac{dL}{dy_{21}} &\frac{dL}{dy_{22}} 
\end{pmatrix} $

위와 같이 연산의 결과는 y, 계산 그래프를 타고 전달되는 역전파의 값은 dout으로 나타냈다.

이제 $ \frac{dL}{dx_{21}} $의 계산을 살펴보겠다.

Chain rule에 의해 $ \frac{dL}{dx_{21}} $는 다음 수식으로 계산된다. 

$ \frac{dL}{dx_{21}} = \Sigma\Sigma{\frac{dL}{dy_{ij}} \frac{dy_{ij}}{dx_{21}}} $

이때 $\frac{dy_{ij}}{dx_{21}}$는 $ y_{ij}$의 계산에 $ x_{21}$이 포함되지 않은 경우 0, 포함된 경우는 $ x_{21}$과 곱해진 weight 이므로, ($ y$의 수식을 직접 미분)

위 수식을 풀어쓰면 다음과 같이 미분값을 얻을 수 있다.

$ \frac{dL}{dx_{21}} = \Sigma\Sigma{\frac{dL}{dy_{ij}} \frac{dy_{ij}}{dx_{21}}}
= \frac{dL}{dy_{11}}*w_{21} +\frac{dL}{dy_{12}}*0 + \frac{dL}{dy_{21}}*w_{11} + \frac{dL}{dy_{22}}*0 $

즉, $ \frac{dL}{dx_{21}} $는 '$ x_{21}$이 영향을 끼친(계산에 포함된) $ y_{ij}$의 역전파값($ \frac{dL}{d_y{ij}}$)과 그때 $ x_{21}$과 곱해진 weight의 곱의 합'이 된다.

전체 $ \frac{dL}{dx}$를 계산하기 위해서는 $ x_{21}$을 $ x_{rc}$로 일반화시키기만 하면 된다.

$ \frac{dL}{dw}$를 구하는 과정도 위 과정과 동일하다.

<Spatial Batch Normalization>

CNN에서 batch normalization을 적용하려면 mean과 std를 channel에 대해 계산해야 한다. 

channel 별로 통계를 내는 이유는 같은 channel이 같은 weight(filter)의 영향을 받았기 때문이다.

(과제에서 간단하게 소개된 개념이라, 자세한 개념은 실제 spatail batch normalization 논문을 참고하는 것을 추천합니다.)

Batch normalization의 구현도 복잡했기 때문에 구현에 앞서 걱정이 앞섰지만, 

주석으로 제공된 hint를 이용하여 비교적 간단하게 구현할 수 있었다.

앞서 구현한 batch normalization을 그대로 이용하면 된다.

다만 적용하기 위해 shape를 바꾸는 과정의 코드가 꽤 복잡했다.

위와 같은 3x3x2x2 (NxCxHxW) 크기의 matrix를 통해 처리 과정을 정리해보겠다.

channel 별로 mean과 std를 구한 후 normalization을 수행해야 하므로, 

matrix를 다음과 같이 변경해야 한다. 

위와 같이 변경하면 각 row별로 일반적인 batch normalzation을 적용하면 된다.

Batch Normarlization 구현 상 row별로 하나의 데이터이므로, 정확히는 위 matrix에 transpose까지 적용해줘야 된다.

그러나 일반적인 reshape 만으로는 위와 같이 변경할 수 없었고,

reshape와 np.concatenate 두 가지 방식을 적용하여 변경이 가능했다.

먼저 reshape이다. 

NxCx(H*W)의 형태로 reshape하면 다음과 같이 변경된다. 

각 데이터 별로 channel의 matrix는 vector로 reshape되었다. 그림으로 나타내면 다음과 같은 상태이다.

이제 3개의 결과를 row-wise로 이어붙여주기만 하면 되고, 해당 내용은 'np.concatenate( ~, axis = 1)' 코드로 구현이 가능했다.

Concatenate를 수행하고 trasnpose까지 적용한 결과이다. 

위 matrix에 대해서는 일반적인 batch normarlization을 적용할 수 있다. 

다만 그 결과를 다시 NxCxHxW shape으로 변경시켜주어야 하는데, 해당 내용은 반대의 순서대로 split과 reshape를 적용하면 된다.

최종 코드이다.

4줄의 코드로 spatial batch normalization의 구현이 가능하다.

Backward 연산의 경우에도 batchnorm_backward가 사용된다는 점을 제외하고 사실상 동일하다.

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Assignment2 에서는 코드보다는 진행했던 실험에 대한 결과와 구현 시 어려웠던 점을 중점적으로 정리할 예정이다.

<Batch Normalization>

https://vstylestdy.tistory.com/38

Batch normalization에 대해 강의에서 다룬 내용을 정리해둔 글이다.

이론적 내용은 위 글을 참고 하면 되겠다.

Q2에서는 batch normalization layer를 구현하는 내용을 진행하였다.

Affine이나 ReLU 등을 layer로 구현하여 forward, backward 연산을 구현한 것처럼 batch normalization에 대해서도 forward, backward를 구현하면 된다. 

그 중 역전파를 계산하는 과정이 복잡했어서 해당 내용에 대해 정리하겠다.

BN back propagation

먼저 batch normalization을 계산 그래프로 표현하면 다음과 같다. 

평균을 구하는 mean이나 표준편차를 계산하는 std 등이 일반적이진 않지만, 위 계산 그래프를 바탕으로 역전파를 계산하면 backward()의 수식을 구현할 수 있다.

또 하나 주의할 점은 행렬 간의 미분이 필요하다는 점이다.

https://vstylestdy.tistory.com/35

Assignment1 에서 affine layer의 역전파를 구현할 때 사용했던 방법을 그대로 적용했다.

직접적으로 미분을 구하기 보다는 chain rule을 이용한다.

우선 $ \frac{dL}{dx'} $까지의 역전파 과정을 나타내면 다음과 같다.

(편의상 $ \hat x$를 x'으로 나타내었다.)

앞서 말했듯이 affine layer때 역전파를 계산한 것처럼 chain rule을 적용하여 계산하면 된다.

위 과정 중에서 $\frac{dL}{dx'} $이 r*dout이 되는 과정에 대해서만 chain rule을 통해 계산하는 법을 적용해보겠다.

gamma나 beta에 대한 미분도 동일한 원리를 적용하면 쉽게 유도할 수 있을 것이다. 

$\frac{dL}{dx'} = r*dout$ 유도

$x'$과 $r$의 곱을 $t$라고 하고, dout을 통해 전달되는 값($ \frac{dL}{dy}$)의 i행 j열을 $ o_{ij}$라고 표현하겠다.

(역전파 계산은 생략되었지만, $ \frac{dL}{dy} = \frac{dL}{dt}$ 이다.)

$ \frac{dL}{dx'_{11}}$의 미분만 살펴보면, 위와 같이 계산된다. Matrix 사이의 dot은 element-wise 곱을 의미한다.

※ 수식 자체에서 matrix가 사용되는 것은 아니고, scalar간의 합을 한 번에 표현하기 위해서 위와 같이 표현했다.

(좌측의 시그마와 동일한 표현이다.) 

$ \frac{dt_{11}}{dx'_{11}}$을 제외한 미분 값은 모두 0이 되므로 $ r_1$과 $ o_{11}$의 곱으로 정리된다.

동일한 원리로 나머지 원소의 미분값을 계산하면 $ \frac{dL}{dx'}$은 다음과 같이 $ dout*r$이 된다.

$ \frac{dL}{dx'}$ 이후의 역전파는 다음과 같이 계산된다. 

마지막의 $ \frac{dL}{dx}$는 3가지로 갈라진 곳에서 전달되는 역전파를 모두 합하면 된다.

이번 역전파의 계산도 모두 chain rule을 기반으로 계산하였고, root나 역수 등으로 인해 계산이 조금 껄끄러워지고 식이 복잡해지긴 했지만 그 원리는 동일하다.

평균을 구하는 mean 노드와 표준편차를 구하는 std 노드는 조금 새로운데, 막상 계산해보면 특이할 것은 없다.

'mean' 노드의 역전파만 조금 더 자세히 살펴보겠다. 

Mean 노드의 역전파

먼저 x, u와 역전파를 전달되는 값은 위와 같이 표현하겠다.

마찬가지로 $ \frac{dL}{dx_{11}}$을 먼저 살펴보면, 다음 식이 성립한다.

위 예시에 대해서는 n = 2겠지만 $ u$는 평균으로 계산되는 값이므로 일반화하여 n으로 표현하였다. 

같은 방식으로 모든 $ x$에 대해 계산하면, $ \frac{dL}{dx}$는

위와 같다.

(k는 전달되는 역전파 값이며, 다른 방향에서 계산되는 $ \frac{dL}{dx}$ 값과 더해져야 최종적인 미분이 계산된다.)

표준 편차를 계산하는 루트로 흐르는 역전파의 계산도 같은 원리로 계산할 수 있다.

실험 - with BN vs without BN

Forward와 backward를 모두 추가하여 batch normalizaton layer를 구현한 후, 

실제로 affine layer와 ReLU 사이에 해당 layer를 추가한 후 train 과정을 비교하는 실험을 진행했다.

BN을 추가한 상태로는 10 epoch로 loss가 1 정도로 감소하였다.

BN을 적용하지 않았을 때는 10 epoch로 loss가 1.4 정도까지만 감소하였다.

파란색으로 표현된 결과가 BN을 적용한 결과, 주황색으로 표현된 결과가 BN을 추가하지 않은 결과이다. 

더 빠르게 수렴하는 것을 확인할 수 있다. 

이번엔 다양한 weight initialization에 대해 BN을 적용한 경우와 BN을 적용하지 않은 경우를 비교한 실험이다.

BN을 적용한 경우에는 initialization의 영향을 훨씬 덜 받는다.

실험 - Batch size의 영향

Batch size를 다양하게 한 후 학습 과정을 비교한 결과이다. baseline은 BN을 적용하지 않은 경우이다. 

먼저 실험 결과를 살펴보면, batch size가 클수록 training accuracy가 더 빨리 증가하는 모습을 보인다.

그러나 validation accuracy의 경우에는 큰 차이를 보이지 않는다. 

관련 내용을 찾아본 결과,

기본적으로 batch size가 클수록 batch의 통계가 전체 training data의 통계에서 크게 벗어나지 않을 확률이 커지기 때문에, 더 빠르게 수렴하고 좋은 성능을 보이는 것이 맞다고 한다.

반대로 batch size가 작은 경우 수렴은 덜 안정이지만, 일종의 regularization 효과를 준다고 한다.  

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 10에서는 기본적인 RNN 구조와 비전 영역에서의 RRN 활용 그리고 LSTM 등에 대해 다루고 있다.

<Recurrent Neural Networks, RNN>

RNN은 sequences를 다루기 위해 개발된 구조이다.

기존의 모델은 하나의 input에 대해 하나의 출력을 갖는 one to one 구조였지만,

RNN은 다음과 같은 구조를 갖는다.

수행하려는 tasks에 따라 다양한 수의 input과 output을 갖을 수 있다.

- one to many

ex) 하나의 input 이미지에 대해 설명 하는 문장(여러 단어) 출력, image captioning

- many to one

ex) 문장(여러 단어)을 보고 긍정, 부정 등 분석을 출력, sentiment classification

- many to many

ex) 문장에서 문장을 생성, 기계 번역

- many to many

ex) 동영상에서 여러 개의 frame마다 분석 수행, video classification on frame level

- non-sequence data

Sequence data가 아닌 경우에도 RNN을 사용할 수 있다. 

예를 들어, 픽셀을 순차적으로 처리하며 이미지를 생성하는 것도 가능하다.

(강의에서는 mnist dataset을 생성하는 예시 동영상을 제공한다.)

- Architecture

RNN에는 input vector 뿐만 아니라, hidden state(vector)라는 것이 추가되어,

input과 hidden state를 input으로 출력을 계산한다.

수식을 조금 더 자세히 살펴보면 다음과 같다.

$ h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$

$ y_t = W_{hy}h_t $

(3가지 weight matrix가 서로 다름에 주의)

계산한 state가 다음 출력을 위한 input으로 입력되는 형태이다. 

재귀적으로 표현된 그래프를 풀어서 계산 그래프의 형태로 나타내면 다음과 같다. 

계산된 hidden vector를 바탕으로 y를 출력할 수도 있고 그렇지 않을 수도 있다. 이는 task에 따라 달라진다.

Many to many task라면 각 hidden state마다 output을 출력할 것이고, many to one task라면 맨 마지막의 hidden state만을 이용해 출력을 만들어낼 것이다.

Many to many task의 경우 loss는 위와 같이 계산될 것이다.

RNN을 이용하여 prefix가 주어졌을 때 다음으로 어떠한 문자가 출력되어야 하는지 예측하는 예시이다. 

문자를 {h, e, l, o}로 한정시키고, 각각의 문자는 one-hot encoding을 통해 vector로 대응시켰다.

$ h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$

$ y_t = W_{hy}h_t $

앞서 살펴본 위 식을 바탕으로 계산하면 hidden layer와 ouptut layer가 계산된다. 

현재 그림에서 앞의 input에 대해서는 잘못된 예측을 수행하고 있긴 하지만, 마지막의 'l'에 대해서는 제대로 'o'를 예측하고 있다.

$ W_{hy}, W_{hh}, W_{xh}$가 적절하게 학습되면 앞의 layers도 정확해질 것이다.

RNN in test time

RNN에서는 종종 어떠한 class에 대한 확률이 가장 높게 출력되더라도 test time에는 가장 높은 확률을 가진 값을 출력하는 것이 아니라, 'sample'하는 방식(확률을 출력될 확률로 해석)으로 출력을 선택한다. 

이렇게 함으로써 좀 더 다양한 출력을 생성할 수 있다. 

Truncated Backpropagation

RNN에서는 sequences를 다루다보니 sequences가 매우 길어지는 경우 역전파를 계산하는 것에 엄청난 연산이 필요하다.

따라서 일정 길이마다 구분하여 loss를 계산하는 기법이 truncated backpropagtion이다.

Applications

RNN을 다양한 데이터에 train시킨 결과를 보여주고 있다.(prefix로 다음 단어를 출력하는 RNN 모델)

셰익스피어의 책을 학습시키면 유사하게 글을 생성하고, C 코드를 학습시키면 그럴듯한 C 코드를 생성한다.

학습 데이터로 부터 이러한 문자 이후에는 이러한 문자가 나올 것이다라고 학습한 것이기 때문에,

모양은 그럴듯 하지만 정상적인 code는 아니다.

Interpretation

CNN에서 각 filter가 직선이나 edge같은 feature를 학습하는 것처럼, RNN에서의 hidden vectors도 해석 가능한 feature를 학습한다고 한다(항상 해석 가능한 것은 아니다.). 

Vector에서 특정 element마다 특정 역할을 수행하는 방식이다. 

예를 들어, 2번째 element가 큰 값을 출력할 수록 현재 큰 따옴표안에서 글을 쓰고 있음을 의미하는 것이고, 

4번째 element가 작은 값을 출력할 수록 문장을 끝내야할 시점이 다가온다는 것을 의미하는 등의 방식이다.

실제 training 결과 어떠한 element가 큰 따옴표를 detect하는 결과이다.

해당 element의 출력이 클수록 파란색에 가깝게 나타냈다.

Image Captioning

이미지에 대해 설명하는 문장을 출력하는 task를 image captioning이라고 한다. 

먼저 image는 CNN의 input으로 입력되고, CNN의 출력 결과가 RNN에 주어지는 형태로 image captioning을 수행할 수 있다. 

Image Captioning with Attention

Image captioing을 수행할 때 attention을 이용할 수도 있다고 한다. 

강의에서도 개념적인 응용에 대해서 설명하고 있어 자세한 동작은 알 수 없지만, 

기존 image captioning에서는 CNN의 결과가 RNN으로 전달된 후 RNN의 각 layer마다 단어를 출력하지만,

attention을 이용하는 방식에서는 단어와 attention을 모두 출력하여 attention을 이미지에 적용한 후 다시 input으로 사용하는 구조인 것으로 보인다. 

<Multilayer RNN>

RNN을 잘 알지는 못했지만, 기존에도 대략적인 설명을 보게되면 항상 layer가 하나인 것에 의문이 있었는데, 

실제로 layer의 depth가 2개 이상인 multilyaer RNN도 존재한다고 한다. 

자세한 동작에 대해서는 다루지 않고 소개하는 정도로만 다루고 있다.

<LSTM, Long Short Term Memory>

RNN의 문제

LSTM에 대해 살펴보기에 앞서 먼저 일반적인 RNN의 문제를 살펴보자.

역전파가 전개되는 과정을 나타낸 그림으로, 빨간색으로 나타난 길로 흐르는 역전파를 생각해보면 계속해서 $ W^T$가 곱해지게 된다. 

W가 scalar라고 생각해보면 W가 1보다 큰값이라면 sequence가 길어질수록 gradient값은 폭발할 것이고, 

W가 1보다 작은 값이라면 gradient값은 0에 수렴할 것이다. 

편의를 위해 scalar인 경우를 생각해봤지만 W가 matrix인 경우에도 동일한 문제는 발생한다.

W가 1보다 커서 exploding gradients가 발생하는 경우에는 gradient clipping이라는 기법을 통해 해결하기도 한다.

매번 값이 정해둔 threshold보다 커질때마다 scale을 해주는 방식이다.

그러나 gradient vanishing 문제는 구조적 문제를 해결하지 않고서는 해결하기 어려웠다.

Gradient vaninshing 문제를 해결하기 위해 새롭게 등장한 구조가 LSTM이다.

Architecture

그림이 조금 복잡해보인다. 기본적으로 RNN과 동일한 구조를 갖지만,

hidden state에 이어 Cell state, $ C_t$까지 추가되었다고 생각하면 된다.

$ c_t$와 $ h_t$의 계산은 다음과 같고, 

 두 state에 계산되는 $ i, f, o, g$의 계산은 다음과 같다. 

수식이 복잡해 보이는데, 

(1) W와 $ h_{t-1}$과 $ x_t$를 이어붙인 vector를 곱해주고, 

(2) $i, f, o$에 대해서는 sigmoid, $ g$에 대해서는 tanh를 적용해서 계산해준다는 의미이다. 

여기에서 사용되는 $ i, f, o, g$의 의미는 다음과 같다.

 - $ i$

 Cell에 추가할지 말지를 결정

 - $ f$

 전달된 cell을 얼마나 forget할지

 - $ o$

 Cell의 정보를 얼마나 노출할지(hidden state로 전달할지)

 - $ g$

 Cell에 얼마나 더 입력할 지

 (유일하게 tanh를 적용한 결과로, -1 ~ 1까지의 값을 같는다.)

위 의미를 바탕으로 수식을 다시 한 번 살펴보면 LSTM에서 어떠한 계산을 하는 것인지 조금 더 이해할 수 있다.

Cell state는 이전의 cell state보다 $ f$만큼 약해지고, $ i$와 $g$이 element-wise 곱이 보충되며,

hidden state는 cell state를 얼마나 들어낼지 $ o$에 의해 결정된다. 

사실 위 내용만으로 LSTM이 어떻게 동작하는지 해석하기에는 어려움이 있지만,

앞서 얘기했듯이 gradient vanishing 문제를 해결할 수 있다는 구조적인 장점을 집중적으로 살펴보자.

Cell state로 흐르는 gradient의 이동은 빨간색 화살표를 따른다.

역전파 과정을 살펴보면, tanh를 거치는 과정은 RNN과 동일하고, '+'는 역전파를 방해하지 않는다.

RNN과 차이가 발생하는 부분은 W대신 $ f^T$를 곱해주게 된다는 점이다.

f는 각 단계마다 input(x와 이전 단계의 hidden state)과 W의 곱으로 생성되는 고정되지 않은 값이다.

따라서 RNN과 달리 계속 같은 수($ W^T$)를 곱해주는 것과 달리, 매번 다른 값을 곱해주기 때문에 gradient vanishing 문제가 발생하지 않는다.

결국 중요한 것은 Weight에 대한 미분인데, W에 대한 미분의 계산에도 cell state로 전달된 역전파 값이 사용되므로, cell state로 전달되는 역전파가 잘 전달되면 W의 미분도 잘 이뤄진다. 

이러한 점에서 ResNet과 유사하다고도 볼 수 있으며, 둘의 중간 단게로 highway networks 라는 것도 존재한다고 한다.