AI

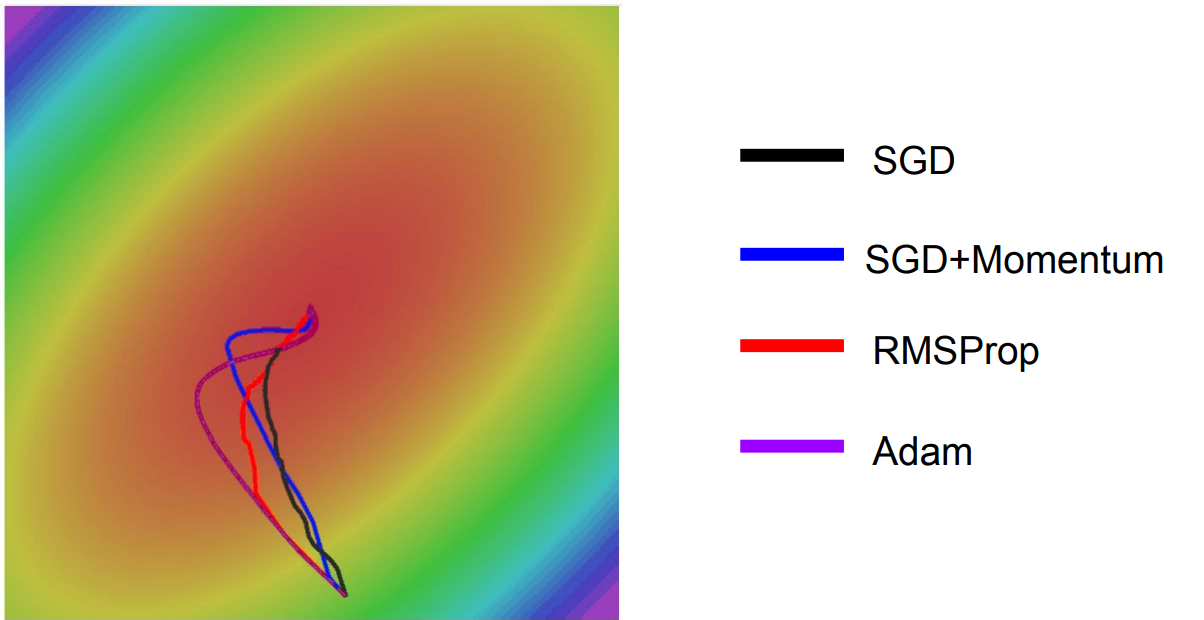
※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 10에서는 기본적인 RNN 구조와 비전 영역에서의 RRN 활용 그리고 LSTM 등에 대해 다루고 있다.

<Recurrent Neural Networks, RNN>

RNN은 sequences를 다루기 위해 개발된 구조이다.

기존의 모델은 하나의 input에 대해 하나의 출력을 갖는 one to one 구조였지만,

RNN은 다음과 같은 구조를 갖는다.

수행하려는 tasks에 따라 다양한 수의 input과 output을 갖을 수 있다.

- one to many

ex) 하나의 input 이미지에 대해 설명 하는 문장(여러 단어) 출력, image captioning

- many to one

ex) 문장(여러 단어)을 보고 긍정, 부정 등 분석을 출력, sentiment classification

- many to many

ex) 문장에서 문장을 생성, 기계 번역

- many to many

ex) 동영상에서 여러 개의 frame마다 분석 수행, video classification on frame level

- non-sequence data

Sequence data가 아닌 경우에도 RNN을 사용할 수 있다. 

예를 들어, 픽셀을 순차적으로 처리하며 이미지를 생성하는 것도 가능하다.

(강의에서는 mnist dataset을 생성하는 예시 동영상을 제공한다.)

- Architecture

RNN에는 input vector 뿐만 아니라, hidden state(vector)라는 것이 추가되어,

input과 hidden state를 input으로 출력을 계산한다.

수식을 조금 더 자세히 살펴보면 다음과 같다.

$ h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$

$ y_t = W_{hy}h_t $

(3가지 weight matrix가 서로 다름에 주의)

계산한 state가 다음 출력을 위한 input으로 입력되는 형태이다. 

재귀적으로 표현된 그래프를 풀어서 계산 그래프의 형태로 나타내면 다음과 같다. 

계산된 hidden vector를 바탕으로 y를 출력할 수도 있고 그렇지 않을 수도 있다. 이는 task에 따라 달라진다.

Many to many task라면 각 hidden state마다 output을 출력할 것이고, many to one task라면 맨 마지막의 hidden state만을 이용해 출력을 만들어낼 것이다.

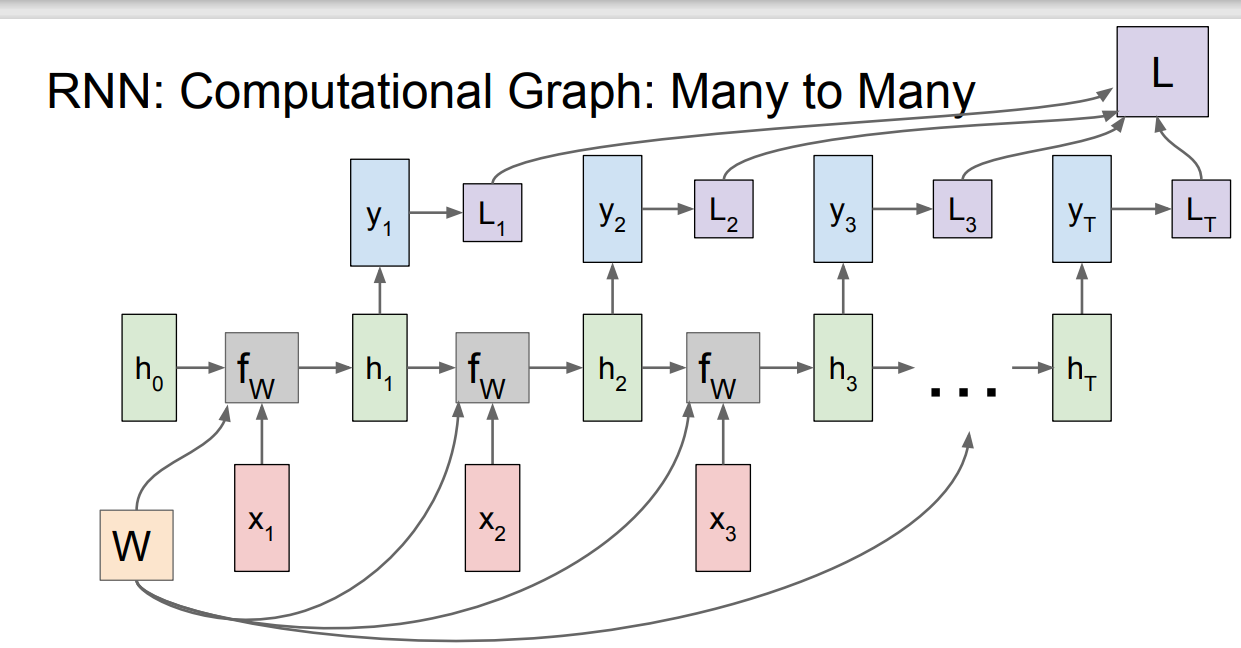
Many to many task의 경우 loss는 위와 같이 계산될 것이다.

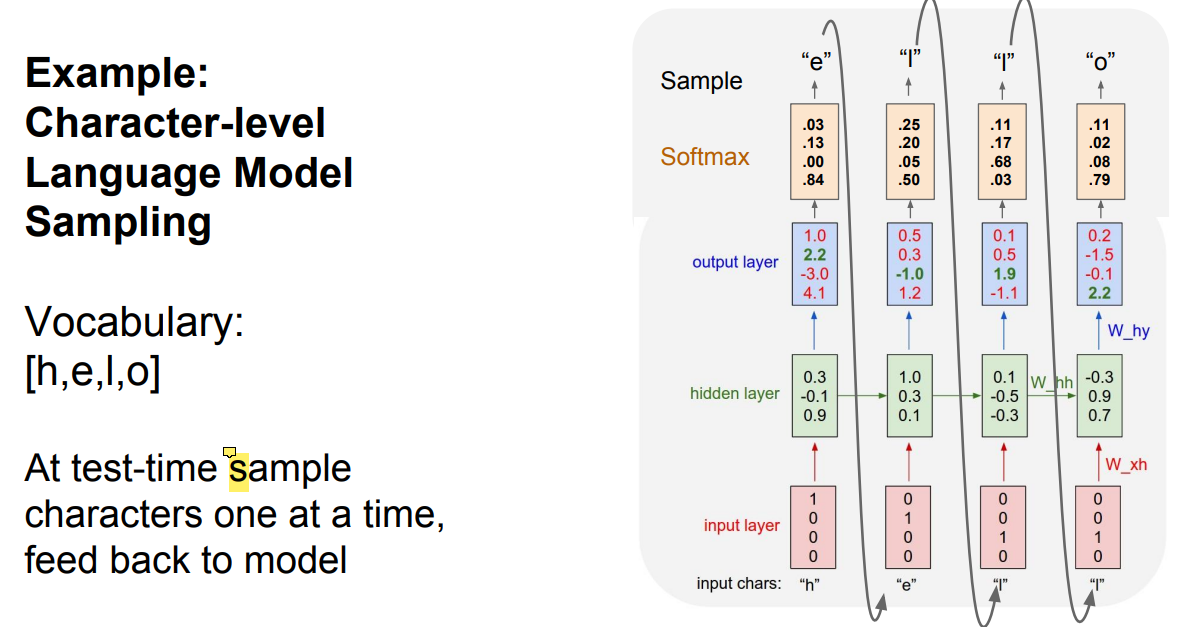
RNN을 이용하여 prefix가 주어졌을 때 다음으로 어떠한 문자가 출력되어야 하는지 예측하는 예시이다. 

문자를 {h, e, l, o}로 한정시키고, 각각의 문자는 one-hot encoding을 통해 vector로 대응시켰다.

$ h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$

$ y_t = W_{hy}h_t $

앞서 살펴본 위 식을 바탕으로 계산하면 hidden layer와 ouptut layer가 계산된다. 

현재 그림에서 앞의 input에 대해서는 잘못된 예측을 수행하고 있긴 하지만, 마지막의 'l'에 대해서는 제대로 'o'를 예측하고 있다.

$ W_{hy}, W_{hh}, W_{xh}$가 적절하게 학습되면 앞의 layers도 정확해질 것이다.

RNN in test time

RNN에서는 종종 어떠한 class에 대한 확률이 가장 높게 출력되더라도 test time에는 가장 높은 확률을 가진 값을 출력하는 것이 아니라, 'sample'하는 방식(확률을 출력될 확률로 해석)으로 출력을 선택한다. 

이렇게 함으로써 좀 더 다양한 출력을 생성할 수 있다. 

Truncated Backpropagation

RNN에서는 sequences를 다루다보니 sequences가 매우 길어지는 경우 역전파를 계산하는 것에 엄청난 연산이 필요하다.

따라서 일정 길이마다 구분하여 loss를 계산하는 기법이 truncated backpropagtion이다.

Applications

RNN을 다양한 데이터에 train시킨 결과를 보여주고 있다.(prefix로 다음 단어를 출력하는 RNN 모델)

셰익스피어의 책을 학습시키면 유사하게 글을 생성하고, C 코드를 학습시키면 그럴듯한 C 코드를 생성한다.

학습 데이터로 부터 이러한 문자 이후에는 이러한 문자가 나올 것이다라고 학습한 것이기 때문에,

모양은 그럴듯 하지만 정상적인 code는 아니다.

Interpretation

CNN에서 각 filter가 직선이나 edge같은 feature를 학습하는 것처럼, RNN에서의 hidden vectors도 해석 가능한 feature를 학습한다고 한다(항상 해석 가능한 것은 아니다.). 

Vector에서 특정 element마다 특정 역할을 수행하는 방식이다. 

예를 들어, 2번째 element가 큰 값을 출력할 수록 현재 큰 따옴표안에서 글을 쓰고 있음을 의미하는 것이고, 

4번째 element가 작은 값을 출력할 수록 문장을 끝내야할 시점이 다가온다는 것을 의미하는 등의 방식이다.

실제 training 결과 어떠한 element가 큰 따옴표를 detect하는 결과이다.

해당 element의 출력이 클수록 파란색에 가깝게 나타냈다.

Image Captioning

이미지에 대해 설명하는 문장을 출력하는 task를 image captioning이라고 한다. 

먼저 image는 CNN의 input으로 입력되고, CNN의 출력 결과가 RNN에 주어지는 형태로 image captioning을 수행할 수 있다. 

Image Captioning with Attention

Image captioing을 수행할 때 attention을 이용할 수도 있다고 한다. 

강의에서도 개념적인 응용에 대해서 설명하고 있어 자세한 동작은 알 수 없지만, 

기존 image captioning에서는 CNN의 결과가 RNN으로 전달된 후 RNN의 각 layer마다 단어를 출력하지만,

attention을 이용하는 방식에서는 단어와 attention을 모두 출력하여 attention을 이미지에 적용한 후 다시 input으로 사용하는 구조인 것으로 보인다. 

<Multilayer RNN>

RNN을 잘 알지는 못했지만, 기존에도 대략적인 설명을 보게되면 항상 layer가 하나인 것에 의문이 있었는데, 

실제로 layer의 depth가 2개 이상인 multilyaer RNN도 존재한다고 한다. 

자세한 동작에 대해서는 다루지 않고 소개하는 정도로만 다루고 있다.

<LSTM, Long Short Term Memory>

RNN의 문제

LSTM에 대해 살펴보기에 앞서 먼저 일반적인 RNN의 문제를 살펴보자.

역전파가 전개되는 과정을 나타낸 그림으로, 빨간색으로 나타난 길로 흐르는 역전파를 생각해보면 계속해서 $ W^T$가 곱해지게 된다. 

W가 scalar라고 생각해보면 W가 1보다 큰값이라면 sequence가 길어질수록 gradient값은 폭발할 것이고, 

W가 1보다 작은 값이라면 gradient값은 0에 수렴할 것이다. 

편의를 위해 scalar인 경우를 생각해봤지만 W가 matrix인 경우에도 동일한 문제는 발생한다.

W가 1보다 커서 exploding gradients가 발생하는 경우에는 gradient clipping이라는 기법을 통해 해결하기도 한다.

매번 값이 정해둔 threshold보다 커질때마다 scale을 해주는 방식이다.

그러나 gradient vanishing 문제는 구조적 문제를 해결하지 않고서는 해결하기 어려웠다.

Gradient vaninshing 문제를 해결하기 위해 새롭게 등장한 구조가 LSTM이다.

Architecture

그림이 조금 복잡해보인다. 기본적으로 RNN과 동일한 구조를 갖지만,

hidden state에 이어 Cell state, $ C_t$까지 추가되었다고 생각하면 된다.

$ c_t$와 $ h_t$의 계산은 다음과 같고, 

 두 state에 계산되는 $ i, f, o, g$의 계산은 다음과 같다. 

수식이 복잡해 보이는데, 

(1) W와 $ h_{t-1}$과 $ x_t$를 이어붙인 vector를 곱해주고, 

(2) $i, f, o$에 대해서는 sigmoid, $ g$에 대해서는 tanh를 적용해서 계산해준다는 의미이다. 

여기에서 사용되는 $ i, f, o, g$의 의미는 다음과 같다.

 - $ i$

 Cell에 추가할지 말지를 결정

 - $ f$

 전달된 cell을 얼마나 forget할지

 - $ o$

 Cell의 정보를 얼마나 노출할지(hidden state로 전달할지)

 - $ g$

 Cell에 얼마나 더 입력할 지

 (유일하게 tanh를 적용한 결과로, -1 ~ 1까지의 값을 같는다.)

위 의미를 바탕으로 수식을 다시 한 번 살펴보면 LSTM에서 어떠한 계산을 하는 것인지 조금 더 이해할 수 있다.

Cell state는 이전의 cell state보다 $ f$만큼 약해지고, $ i$와 $g$이 element-wise 곱이 보충되며,

hidden state는 cell state를 얼마나 들어낼지 $ o$에 의해 결정된다. 

사실 위 내용만으로 LSTM이 어떻게 동작하는지 해석하기에는 어려움이 있지만,

앞서 얘기했듯이 gradient vanishing 문제를 해결할 수 있다는 구조적인 장점을 집중적으로 살펴보자.

Cell state로 흐르는 gradient의 이동은 빨간색 화살표를 따른다.

역전파 과정을 살펴보면, tanh를 거치는 과정은 RNN과 동일하고, '+'는 역전파를 방해하지 않는다.

RNN과 차이가 발생하는 부분은 W대신 $ f^T$를 곱해주게 된다는 점이다.

f는 각 단계마다 input(x와 이전 단계의 hidden state)과 W의 곱으로 생성되는 고정되지 않은 값이다.

따라서 RNN과 달리 계속 같은 수($ W^T$)를 곱해주는 것과 달리, 매번 다른 값을 곱해주기 때문에 gradient vanishing 문제가 발생하지 않는다.

결국 중요한 것은 Weight에 대한 미분인데, W에 대한 미분의 계산에도 cell state로 전달된 역전파 값이 사용되므로, cell state로 전달되는 역전파가 잘 전달되면 W의 미분도 잘 이뤄진다. 

이러한 점에서 ResNet과 유사하다고도 볼 수 있으며, 둘의 중간 단게로 highway networks 라는 것도 존재한다고 한다. 

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 9 에서는 다양한 CNN model을 다루고 있다.

2017년 강의이다 보니 최근 model들은 포함되지 않았지만, ResNet 등 최근 model 들의 기반이 되는 model을 살펴볼 수 있다.

 - AlexNet

 - VGG

 - GoogLeNet

 - ResNet

에 대해 자세히 다루고 있다. 

<AlexNet>

AlexNet은 ImageNet challenge 2012의 winner로, 최초의 CNN 기반 model winner이다.

기본 CNN model의 구조를 정교화 한 모델로, 이후에 다룰 GoogLeNet이나 ResNet에 비해서는 간단한 model이다. 

Conv layers와 Pooling layers 적절히 배치하고, 마지막에 FC layers를 추가한 비교적 단순한 구조이다.

그림을 보면 같은 layer라도 depth를 기준으로 2파트로 나눠져있는데, 이는 2개의 GPU를 training에 사용했음을 나타낸다.

그 외에 자세한 사항은 slide의 내용과 같고, ReLU를 처음으로 사용했다는 점이 눈여겨볼만 하다. 

2013년의 winner인 ZFNet도 AlexNet의 hyperparameters를 개선한 모델이다.

<VGGNet>

2014년에 ImageNet classification에서 2위를 차지한 모델이다.

1위는 GoogleNet이 차지했지만, 다른 task에 대해서는 VGGNet이 더 좋은 성능을 보이는 경우도 있었다고 한다.

VGGNet도 마찬가지로 기존의 CNN model의 틀을 크게 벗어나지는 않는다.

일반적으로 layer를 deeper하게 하는 방향으로 model들은 발전했고,

VGGNet도 layers를 깊게 쌓는 방식으로 좋은 성능을 달성했다.

16 or 19개의 layers를 갖는다.(AlexNet : 8 layers)

VGG의 핵심은 3 x 3 convolution layers를 연속으로 사용해서 층을 깊게 만들었다는 점이다.

작은 filter를 연속으로 사용하는 것의 장점은 무엇일까?

3x3 conv(stride = 1)를 3개 연속으로 쌓는 경우를 예시로 생각해보자.

해당 경우와 하나의 7x7 conv layer는 effective receptive field가 동일하다.

filter별로 처리하는 영역의 크기가 같다는 의미이다.

역으로 7x7크기의 이미지가 하나의 7x7 filter를 거치는 경우와 3개의 3x3 filter(stride = 1)을 연속으로 거치는 경우를 생각해보면 그 출력의 크기가 1x1으로 같다는 것을 알 수 있다.

이때 작은 filter를 연속으로 쌓는 것의 장점은 다음과 같다.

 - 같은 영역을 처리하지만 더 많은 non-linearity를 부여할 수 있다.

 - 더 적은 수의 parameters가 사용된다. ($ 3*9C^{2} < 49C^{2} $)

추가로 VGGNet의 memory와 parameters는 위와 같다. 

Model을 비교할 때, 성능 뿐만 아니라 두 요소 또한 고려할 요소이다.

<GoogLeNet>

2014년에 ImageNet classification에서 1위를 차지한 모델이다.

일반적인 CNN 모델과는 다른 특이한 구조를 갖는다.

Inception module을 도입했다.

Inception module을 사용하고, FC layers를 제거함으로써 parameters의 수를 줄였다.

Inception module

Inception module의 기본적인 아이디어는 network의 연결을 발전시켜보자는 것이다. 

하나의 layer안에서도 다양한 filter, pooling을 적용하여 multiple recpetive field sizes를 갖는다. 

이때 각 filter를 거친 출력의 output shape(H x W)는 stride를 조정하거나 padding을 이용하여 통일하며,

최종 output은 각 filter의 출력을 depth-wise를 이어붙인 값이 된다.

이때, pooling layer가 포함되기 때문에 output의 출력 depth는 input의 depth보다 커지게 된다.

여러 filter를 적용하고, 계속해서 depth가 커지기 때문에 Naive 방식에서는 계산량이 커지는 문제가 존재한다.

따라서 실제 Inception module에서는 1x1 filter를 적용하여("bottleneck" layers라고 한다) depth를 줄여주는 방식으로 계산량을 줄인다.

최종적인 GoogLeNet의 구조는 다음과 같다.

Conv-Pool 로 이뤄진 stem network를 먼저 거친 후, 여러개의 Inception modules가 stack된 구조이다. 

Auxiliary classification

GoogLeNet에서는 가장 끝 layer에만 classification layers가 추가되는 것이 아니라, 중간 layers의 출력을 이용해서도 classication을 수행하도록 되어있다.

이렇게 함으로써, 층이 깊음에도 불구하고 앞에 있는 layers도 backprop을 통해 학습이 잘 이뤄질 수 있다.

(역전파가 3번 수행되는 것은 아니고, loss 자체가 3개의 classification 결과를 모두 이용하는 것)

<ResNet>

ImageNet classifcation에서 2015년에 winner를 차지한 ResNet이다.

매우 좋은 성능으로 사람의 인지능력을 넘어섰다고 한다.

ResNet의 가장 큰 특징은 층이 매우 깊다는 것이다.

무려 152개의 층을 쌓아서, 14년의 우승자인 GoogLeNet이나 VGG가 22, 19개의 층을 쌓았던 점을 생각하면 엄청난 발전이다. 

이렇게 깊게 층을 쌓을 수 있었던 것은 'residual connections'를 사용한 덕분이다.

한 층의 출력이 다음층으로 뿐만 아니라, 이후의 다른 layer로도 전달이 된다.

Residual connection은 다음과 같은 아이디어를 기반으로 적용되었다. 

먼저 기존에는 층을 너무 깊게 쌓으면 학습이 잘이뤄지지 않는 문제가 있었다. 

Parameters의 수가 많기 때문에 overfitting 문제를 예상할 수 있겠지만, 학습 자체도 제대로 이뤄지지 않아 training error 자체도 낮아지지 않는다.

기본적으로, 층을 더 쌓으면 최소한 추가하기 전보다 같은 성능을 낼 수 있어야한다. 

위 그림에서 H(x)가 prediction을 위한 최상의 output이라고 가정을 하자.

기존의 방식에서는 H(x)를 잘 출력하기 위해 학습한다면,

residual block에서는  input featues와 H(x) 간의 차이, residual을 잘 찾기위해 학습한다(위 그림에서 F(x)가 잔차이다).

즉, input으로 들어온 값에 어떠한 값을 추가해줘야 최적의 성능을 낼 수 있을지를 학습한다.

최소한 잔차가 0이라고 취급하면 input 값이 그대로 전달될 수 있음으로, 층을 더 쌓더라도 최소한 성능이 나빠지지는 않는다는 아이디어이다. 

※ 강의에서는 H(x) 자체가 아니라 residual을 학습하는 이유에 대해서 위와 같이 직관적으로 설명하고 있다.

그 외에도 Residual connection을 통해 gradient vaninshing 문제가 해소되는 것이 층을 깊게 쌓을 수 있는 주요한 이유로 알고 있다.

(1/25 논문 확인 후 수정 : Gradient vanishing/explosion 문제는 batch normalization등으로 해소가 가능하지만,  학습은 되더라도 더 적은 수의 layers보다 성능이 안좋아지는 'degradation'이 문제였고, 해당 문제를 해결한 방법이 residual learning이 맞다.)

최종적으로 사용된 ResNet 모델의 구조는 위와 같다.

VGG에서 처럼 3x3 filter를 연속으로 적용하지만 매우 깊게 설계할 수 있었다.

또 층이 깊으므로 계산의 효율성을 위해 GoogLeNet과 같이 1x1 conv layers를 이용한다.

그 외에 batch noramlization을 적용하는 등의 자세한 사항은 생략되어 있다. 

<모델 비교>

매년 정확도는 좋아지면서 layers는 깊어지는 양상을 확인할 수 있다.

정확도 뿐만 아니라 연산의 수나 parameters의 수, 메모리 용량 등도 성능을 평가할 때 고려해야할 요소이다.

각 모델을 비교한 결과는 위와 같다.

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 8에서는 CPU/GPU 및 deep learning 관련 software, framework를 다루고 있다.

Tensorflow와 Pytorch에 대해 주로 다루고 있다.

※해당 내용은 변화가 빠른 내용이다보니 2017년의 강의 내용이 글을 쓰는 현재 시점과는 차이가 있을 수 있다.

<CPU/GPU>

CPU와 GPU의 대표적인 차이는 cores의 수이다.

CPU는 일반적으로 최대 10개 정도의 core를 갖는다면, GPU의 cores 수는 1000단위로 그 차이는 매우 크다.

따라서 간단한 연산을 병렬로 처리하기에 GPU가 유리하다.

대표적으로 matrix multiplication이나 convolution 연산 등을 떠올릴 수 있고, 모두 deep learning에서 흔하게 쓰이는 연산이다.

다만 개별 core의 성능은 CPU가 훨씬 빠르다.

또한 GPU는 GPU 만의 메모리를 갖고, CPU와 GPU 간의 데이터 이동은 병목현상을 유발할 수 있다는 점도 기억해두어야 한다.

<Deep Learning Frameworks>

기본적으로 deep learning framework는 다음과 같은 편리함을 제공한다.

 - 계산 그래프를 구현

 - Gradients의 계산을 자동으로 제공

 - GPU 상에서 동작하기에 최적화되어 있음

● TensorFlow

2-layer NN을 구현하는 코드를 통해 tensorflow 코드의 기본적인 동작에 대해 살펴보겠다. 

기본적으로 tensorflow는 computational graph의 구조를 작성(①, ②)하는 코드와 실제 계산을 동작시키는 코드(③)가 구분된다.

(※ tf 최근 버전의 경우, Session을 이용하지 않는 것으로 알고 있다.)

① Computational graph의 구조 작성

파란색 사각형으로 표시된 ① 영역은 computational graph를 구현한다. 

변수를 tf.~의 자료형으로 선언하는 것을 제외하고는 어떠한 연산을 수행하는지 어렵지 않게 알 수 있을 것이다.

변수를 numpy 등이 아니라 tf.~로 선언함으로써 GPU 상에서 다룰 수 있게 된다.

x, y의 경우 placeholder, w1, w2의 경우 Variable로 선언되어 있는데, 

이는 w1과 w2는 update가 빈번하게 이뤄지는 변수이기 때문이다.

한 번 graph에 제공되면 그 값이 유지되는 x, y와 다르게 w1, w2는 매번 update되고, 이를 매번 CPU에서 제공하는 것은 큰 overhead를 유발한다(둘의 메모리가 다르기 떄문에, 이동으로 인한 overhead).

따라서 해당 변수를 Variable로 선언하여, GPU 상에서 업데이트가 이뤄지도록 한다.

② Optimizer

Optimizer를 통해서 NN의 train을 매우 간단하게 구현할 수 있다. 

Optimizer의 종류를 선언해주고, optimizer가 어떠한 노드를 최적화할 것인지 전달해주면 자동으로 optimization을 수행한다. 정확히는 weight의 update를 자동으로 수행한다. 

어떠한 parameter를 training할 것인지도 알아서 판단하므로(엄밀히는 trainalbe하게 선언된 변수를 찾아서 train), 

특정 node의 값을 optimize하라는 코드만 작성해도 필요한 parameter를 최적화한다.

③ Training

실제로 계산을 수행할 때는 Session을 생성하고, session을 run 시켜서 계산이 이뤄진다.

즉, 앞선 코드는 구조만을 작성하는 코드이다.

생성한 sess를 실행시키고, 실제 그래프 구조에 적용될 값들을 전달한다.

이 시점에서 w1, w2에 할당될 random 값이 결정된다(global_variable_initializer)).

이 후의 for문이 training을 반복하는 코드이다.

sess.run([loss, updates], feed_dict = values)

loss 노드와 updates 노드를 수행시키면 loss가 계산되기 까지의 computation graph의 노드가 모두 동작하고, updates 노드를 수행시키면 optimization(gradient descent)가 수행된다. 

- High-Level wrapper

자주 쓰이는 layer 들은 보다 high-level로 제공되기도 한다.

앞선 코드와 동일한 역할을 수행하는 코드이며, tf.layers.dense layer를 이용하여 구현할 수도 있다.

Keras

Keras는 훨씬 더 직관적인 high-level wrapper를 구현한다.

매우 직관적이기 때문에 코드만으로 이해하는 것에 어려움은 없다.

그 외에도 다양한 high-level wrappers가 존재한다.

●PyTorch

Abstraction

기본적으로 Pytorch에는 three levels of abstraction이 있다.

 - Tensor : ndarray를 다루는 자료형이고, GPU 상에서 다뤄진다.

 - Varaiable : 계산 그래프의 각 노드이다. Data 뿐만 아니라 gradient도 같이 node에 저장한다.

 - Module : State나 learnable weights를 저장하는 layer이다.

PyTorch의 코드는 조금 더 numpy 형식과 비슷하고, 이해하기 쉽다.

변수를 선언하고(①), 선언한 변수를 통해 필요한 값을 계산한다(②).

'backward()'를 호출하면 해당 노드를 계산하는 데 사용된 노드들의 gradient가 계산되어 각 노드(Variable)에 저장된다.

그 값을 이용해서 업데이트를 수행하면 된다(③). 

Own Autograd

직접 class를 구현하고, backward 연산을 구현해주면 해당 class도 backward()의 역전파 과정에서 자동으로 gradient가 계산된다.

loss.backward()를 호출하면 ReLU() layer의 backward()도 호출이 된다.

PyTorch는 nn을 통해서 higher-level wrapper를 제공한다.

마찬가지로 직관적이기 때문에 코드만으로 쉽게 이해가 가능하다.

PyTroch에서는 nn.Module을 상속해서 새로운 modules를 define할 수 있다.

forward()만 작성해주면 backward()는 autograd를 통해 계산된다. 

실제로 PyTorch 코드를 작성할 때는 위와 같이 하나의 module class로 구현하는 경우가 많다고 한다. 

PyTorch도 마찬가지로 optimization을 간단하게 해주는 기능을 제공한다.

사용할 Optimizer에 업데이트할 parametres와 learning rate를 제공한 후, step()을 호출하면 각 노드에 저장된 grad값을 이용하여 자동으로 업데이트를 수행한다. 

DataLoader는 dataset을 wrap하여 minibatch를 제공하고, shuffle해주는 등의 과정을 간편하면서 효율적으로 동작하도록 해준다.

코드를 통해 활용법을 쉽게 이해할 수 있다.

실제 PyTorch로 코드를 짜는 경우 최종적으로 위와 같은 형태를 자주 보게 될 것이라고 한다.

(하나의 module class로 model을 구현하고, DataLoader로 minibatch를 추출하며 Optimizer를 사용하여 학습을 수행하는 형태)

● Static(TensorFlow) vs Dynamic Graphs(PyTorch)

TensorFlow는 정적으로 계산 그래프를 생성한다. 즉, 계산 그래프를 한 번만 생성하여 계속 이용한다.

PyTorch는 동적으로 계산 그래프를 생성한다. 계산이 필요할 때마다 매 번 그래프를 새로 생성한다.

Static의 장점

- 계산 그래프 최적화

먼저 static 방식의 장점은 그래프의 최적화가 가능하다는 것이다.

같은 연산을 수행하더라도 계산이 조금 더 빠르도록 구조를 바꾸는 등으로 최적화를 수행할 수 있다.

한 번 생성 후 계속 사용할 것이므로, optimization 과정이 조금 걸리더라도 그럴 가치가 있다.

- 직렬화(Serialization)

한 번 생성된 그래프가 계속 사용되므로, 코드가 없더라도 그래프를 직렬화하여 사용할 수 있다.

반면 dynamic 방식은 매 생성마다 코드가 필요하다.

-> 뒤에도 다룰 내용이지만, dynamic 방식은 if문과 같은 일반적인 프로그래밍 구조로 그래프를 생성할 수 있기 때문에 코드가 항상 필요하다.

Dynamic의 장점

- Conditional

바로 위에서 다룬 내용이다.

매번 그래프를 새로 생성하기 때문에 if문과 같은 제어문을 일반적인 코드를 작성하듯이 사용하여 계산 그래프를 생성할 수 있다. 

반면 tensroflow는 일반적인 코드와는 다르게 if문을 사용하는게 아니라 TF 자체에서 제공하는 특별한 operator를 사용해야 한다. -> 해당 operator에 대해 새로 알아야 되며, 코드가 직관적이지 않다.

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 7에서는 fancier optimization, regularization 그리고 transfer learning에 대해 다루고 있다.

<Optimization>

● SGD의 문제점

앞선 강의들에서 training은 보통 SGD를 이용하여 진행하였다. 

그러나 단순 SGD는 몇 가지 문제를 갖는다.

(1) Slow progess

한 feature에 대해서는 loss에 대한 영향(미분)이 크고, 다른 하나의 feature에 대해서는 작다고 가정해보자.

그럼에도 불구하고 두 feature에 대해서 learning rate는 동일하기 때문에, 하나의 learning rate로 서로 loss에 대한 영향력이 크게 차이나는 features를 다루면 위 그림과 같이 한쪽 방향으로 치우친 step을 갖게될 것이다.

그림에서도 직관적으로 확인할 수 있듯이, 이러한 경우 global optima에 비효율적으로 수렴한다. 

(2) stuck

SGD는 local minima나 saddle point를 만나게 되면 더 이상 업데이트하지 않고 stuck하게 된다. 

Gradient descent를 사용하는 모든 알고리즘이 그렇지 않을까 생각이 들었지만,

뒤에서 소개하는 다른 방식들은 gradient descent를 사용함에도 불구하고 미분값이 0인 점에서 stuck하지 않음을 살표볼 수 있다. 

추가로 local minima보다 saddle points가 훨씬 더 흔한 경우라고 한다. 

local optima가 되려면 어느 방향으로 가도 loss가 증가해야 되는데, higher dimension에서 어느 방향으로 가도 증가하는 건 흔하지 않은 일이다. 

(3) gradients from minibatches can be noisy

minibatches를 통해 loss를 계산하는 것이기 때문에 실제 미분값과는 약간의 차이가 존재한다.

따라서 수렴하는 과정자체도 noisy하다.

● SGD + Momentum

우선 수식과 코드를 통해 SGD와 SGD+Momentum 방식이 어떠한 차이를 보이는지 살표보자.

SGD+Momentum 방식은 '속도'의 개념을 최적화 과정에 도입한다. 

속도 = $ \rho$* 현재속도 + 가속도

위치 = 현재 위치 + learning rate*속도

위와 같이 속도를 통해 이동방향과 이동량을 결정하고, 현재의 미분값은 가속도로 속도에 변화를 주는 것과 같이 동작한다. 

(※ 수식을 계속 풀어서 써보면, 결국 속도는 미분값의 weighted sum이다.)

현재 속도의 영향을 감소시키는 $ \rho$, rho는 보통 0.9나 0.99로 설정하는게 흔하다고 한다. 

결론적으로 momentum을 추가함으로써 다음과 같은 효과를 얻을 수 있다.

- stuck을 예방

- 가능한 한 방향을 고집하도록 하여 빠르게 수렴

Nesterove Momentum

일반적인 momentum과 조금 다르게 동작하는 Nesterov momentum 방식도 존재한다.

Gradient를 계산한 후 속도를 업데이트한 후 그 속도로 이동하는 기존 momentum 방식과 다르게,

현재 속도로 이동한 후, 이동한 위치에서 gradient를 계산하고 step을 결정하는 방식으로 동작한다. 

● AdaGrad

마찬가지로 수식을 먼저 살펴보고, 그 동작에 대해 알아보겠다. 

일반적인 SGD와 유사하지만, learning rate와 미분값을 곱한 것을 $ \sqrt{grad^{2}} $로 나눠주는 scaling이 추가되어 있다.

(0으로 나누는 것을 예방하기 위해 1e+7이 더해진 값으로 나눠지기는 한다.)

해당 값으로 나눠줌으로써,

미분값이 큰 방향의 step은 크게 줄여주고, 미분값이 작은 방향의 step은 작게 줄여주는(오히러 가속시킬 수도 있다) 방식으로 step의 scale을  조정한다. 

결국 SGD에서 한쪽 방향으로 크게 진동하며 수렴하던 모습을 예방한다고 생각할 수 있다.

RMSProp

그러나 AdaGrad에는 문제점이 존재한다. 

grad_squared += dx*dx

위 식을 통해 grad_squared는 계속 누적합으로 커지기 때문에 training이 반복되면 

learning_rate*dx / np.sqrt(grad_squared + 1e-7)

의 값은 0에 수렴할 것이다. 

따라서 현재의 grad_squared값에 decay_rate(0 < decay_rate < 1)를 곱해줘서 계속해서 커지는 것을 방지하면서 grad_squred를 계산한다.

● Adam

Adam은 AdaGrad와 Momentum 두 방식을 모두 채용한 방식으로,

대부분의 경우 Adam optimization을 사용하게 될 것이다.

먼저 Bias correction으로 표시된 영역을 제외하고 빨간색과 파란색 사각형으로 표시된 영역을 살표보자.

'first_moment'로 momentum을 계산해주고, momentum 방식대로 업데이트를 수행할 때 'second_moment'를 통해 계산한 RMSProp의 scaling을 수행해주는 방식으로 두 방식을 모두 사용한다. 

Bias correction이 추가되는 이유는 다음과 같다.

second_moment는 0으로 초기화되고, 학습 초기에 second_moment는 0에 근접한 값이다.

따라서 해당 값으로 나눠서 scaling을 해주면 학습 초기의 step은 상당히 커지게 된다. 

따라서 second_moment를 ($ 1-\beta1^{2} $) 으로 다시 한 번 나눠준다.

$ \beta $는 1, 2를 각각 0.9, 0.999로 설정하는 경우가 일반적이라고 한다. 

※ first_moment와 second_moment가 모두 작은 값이니 상쇄되지 않냐는 질문이 있었다.

-> answer : 그럴 수도 있지만, 항상 그런 것은 아니다.

지금까지 다룬 최적화 기법들의 학습 과정을 비교한 예시이다.

- SGD :

약간씩 흔들리며 이동하는 모습을 볼 수 있다. 그림상으로 방향은 좋지만, 해당 방향으로 이동하는 속도는 느리다.

- Momentum :

한 뱡향으로 쭉 갔다가(약간의 over-shooting) 다시 돌아오는 모습이다. 그러나 overshooting 으로 이동하는 속도가 빠르다.

- RMSProp :

over-shooting이 적으면서 비교적 한 방향으로 적절하게 수렴한다.

- Adam :

두 방식의 특징이 모두 나타난다.

Learning Rate, Learning rate decay

앞서 소개한 optimization 방법에서 learning rate는 모두 가장 중요한 hyperparameter이고 적절하게 잘 설정해줘야 한다.

처음 적절한 learning rate를 탐색할 때는 양 끝에서는 최적화에 문제가 있을 정도로 매우 넓은 범위로 탐색해야 좋다고 한다.

Learing rate를 학습하면서 줄이는 방법도 좋은 방법이다.

위와 같은 방법으로 학습하면서 learning rate를 줄일 수 있다.

다만 learning rate decay를 적용하고자 할 때는, learning rate를 먼저 확실하게 설정한 후 적용해야 한다.

특히 Momentum 방식에서 learning rate decay는 중요한 편이다. (Adam에서는 덜 흔하다.)

Second-Order optimization

지금까지는 미분을 수행할 때, linear approximation을 통해 방향을 찾고 learning rate를 통해 보폭을 결정하는 방식으로 최적화를 진행했었다. 

Hessian, quadratic approximaiton을 통해 최적화를 진행하는 방법도 있다. 

Quadratic approximation의 최소값으로 이동하면 되기 때문에, learing rate, hyperpameter가 필요하지 않다.

그러나 hyperparameter가 없다는 장점에도 불구하고, 위 최적화 기법은 deep learning에 적용하기 실용적이지 않다.

Hessian matrix의 크기자체가 $ N^{2}$으로 매우 크고(N : number of parameters), inverting하는 것도 $ O(N^{3})$이 소요된다. 

Approximate inver Hessian을 $ O(n^2)$으로 계산하고, full inverse hessian을 저장하지 않는 L-BFGS라는 방법이 있다고 한다. 

Full batch를 써야 유용하고, non-convex한 경우 잘 동작하지 않기 때문에 마찬가지로 deep learning에서 사용되는 경우는 흔하지 않다고 한다.

-> Full batch를 사용할 수 있다면 시도해볼만 하다.

<Regularization>

Training loss를 줄이는 방향으로 train이 이뤄지지만, 사실 실제로 필요한 것은 새로운 데이터에 대해서 좋은 성능을 보이는 것이다.

우측의 그래프와 같이 training data에 대한 정확도와 validation data에 대한 정확도의 gap이 발생한다면 overfitting 문제를 예상할 수 있고, regularization이 필요하다.

● Model Ensembel

Model ensemble은 여러 개의 독립적인 model을 학습시키고, test time에는 각 model들의 결과를 종합하는 방식이다.

엄청난 성능 증가가 이뤄지지 않지만 확실한 regularization 효과를 얻을 수 있다.

여러 개의 independent한 model을 학습시키는 대신, 하나의 모델의 여러 snapshot을 이용하여 ensemble 효과를 얻을 수도 있다.

하나의 모델을 트레이닝하는 과정에서 다양한 optima에 도달하게 만드는 원리이다. 

실제 parameter 대신 parameter vector의 이동평균을 저장해놓고, test time에는 그 값을 사용하는 Polyak averaging도 존재한다. 

마찬가지로 regularization 효과를 얻을 수 있다. 

● Regularization Term

Loss에 regularzation term을 추가하는 것은 대표적인 regularization 기법이다. 

Weight가 지나치게 커지는 것을 일종의 penalty로 취급하는 방식이다. 

● Dropout

Dropout은 random하게 neuron의 출력을 0으로 만드는 기법이다(정확히는 activation function의 출력을 0으로).

0으로 출력할 확률 또한 hyperparameter이다.

Dropout의 장점은 다음과 같다.

- Co-adaption of features

먼저 하나의 feature에 지나치게 의존하는 것을 예방한다.

예를 들어 현재의 데이터셋에서는 하나의 특징이 classification에 큰 영향을 미친다면 해당 feature에 대해 과적합될 가능성이 있는데, dropout을 함으로써 다양한 feature에 대해 학습을 하게 된다.

- Ensemble

어떠한 neuron을 drop하냐에 따라 모두 다른 구조의 model이라고 볼 수 있고, 

따라서 일종의 ensemble로 인한 regularization 효과를 얻을 수 있다. 

- Test-time

Dropout을 사용하면 nueron의 출력에 확률의 개념이 들어가기 때문에, test-time시의 출력으로 기대값을 출력해야 한다.

그러나 f(x, z)가 매번 달라지는 상황에서 이러한 적분을 게산하는 것은 쉽지 않다.

따라서 이를 approximate하여 설정된 weight의 출력에 dropout possbility를 곱하는 방식으로 출력한다. 

반대로 train time에 neuron의 출력을 p로 나누고 test time에는 그대로 출력하는 inverted dropout도 존재한다.

효과는 결국 동일하면서, test time 시의 성능을 빠르게 하기 위해서이다.

● Common pattern

Regularization의 흔한 패턴은 다음과 같다.

 - Traing time : 일종의 randomness를 추가

 - Test time : Randomness를 평균으로 출력

위의 dropout이 그랬고, lecture 6에서 다룬 batch normalization도 그렇다. 

● Data Augmentation

데이터를 증폭하는 기법으로 다양한 기법이 존재한다. 

 - Image를 좌우반전 시키기

 - Image의 특정 부분을 잘라서 사용하기

 - PCA를 적용하기

등등의 기법이 있다.

Regualrization을 다루다가 data augmentation을 다루는 이유는, data augmentation도 앞서 다룬 common pattern의 효과를 주어 regularization에 도움이 되기 때문이다.

뽑을 수 있는 batch의 조합이 훨씬 다양해지기 때문에 training시에 확률성을 제공하는 효과가 있기 떄문이다. 

● 기타

그 외에도 다양한 기법이 존재한다.

- DropConnect

Dropout과 거의 동일하다.

Neruon의 출력을 0으로 만들었던 dropout과 달리, random weight를 확률적으로 한번씩 0으로 만든다.

- Fractional Max Pooling

Max Pooling을 수행할 때, pooling의 구조를 다양하게 하는 것으로도 training 시에 randomness를 제공하여 regularization 효과를 얻을 수 있다.

- Stochastic Depth

깊은 layer가 있다고 할 때, 아예 random하게 어떤 layer를 없다고 가정하는 방식이다. 

<Trasnfer Learning>

Transfer learning은 CNN을 이용하기 위해서는 매우 많은 데이터가 필요하다는 관념을 반박하는 아이디어이다.

결론적으로 말하면 이미 traing된 모델을 fine tuning하는 방식으로 그렇게 많지 않은 데이터에 대해서 학습이 가능하다는 것이다.

ImageNet과 같은 큰 데이터셋에 학습된 모델을 불러와서, FC layer만 새롭게 학습 시키는 등의 방법을 이용하면 적은 수의 데이터로도 좋은 효과를 기대할 수 있다.

데이터셋이 조금 더 크다면 FC layer 여러 개를 다시 학습하는 등으로 확장할 수 있다.

Transfer learning을 적용할 때 고려할 점이 위의 표에 잘 정리되어 있다.

Transfer learning은 생각보다 훨씬 일반적으로 사용되고 있고, 아예 처음부터 모델을 training하는 경우는 이제 흔하지 않다고 하다.