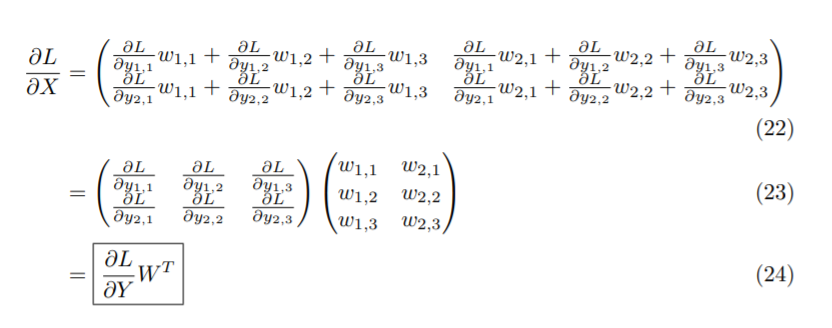AI

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture 6에서는 신경망의 학습에 대해서 다루고 있다.

학습시키기 위해 주의할 점이나 training process 를 다룬다.

- Activation Functions

● Sigmoid

먼저 가장 처음 사용되었고, 대표적인 activation 함수 중 하나인 simoid 함수이다.

Sigmoid 함수를 activation function으로 사용하는 것에는 3가지 문제가 존재한다.

(1) Satureated neurons "kill gradients" -> Gradient vanishing

먼저 gradient vanishing 문제가 존재한다. 

Sigmoid 노드의 local 미분식은 다음과 같다.

$ y = sigmoid(x) $, $ \frac{\partial y}{\partial x} = y(1-y)$

Sigmoid의 값 y는 0과 1 사이이므로 y(1-y) 또한 0과 1사이의 값이다. 

또한 수식을 보지 않더라도 그래프를 보면 대략 x가 10이상, -10 이하만 되더라도 미분값은 거의 0에 수렴하기 때문에 역전파값 또한 0에 수렴하게 된다.

결국 sigmoid를 activation function으로 사용하면, 역전파값이 0에 수렴하고 그 결과 weight의 업데이트가 이뤄지지 않는 문제가 발생하게 된다.

(2) Sigmoid outputs are not zero-centered

Sigmoid의 출력값 자체에도 문제가 있다. 바로 zero-centered되어 있지 않고, 모든 값이 0 이상라는 점이다.

이러한 점이 문제가 되는 이유는 fully connected layer의 역전파를 살펴보면 알 수 있다.

Sigmoid의 출력값이 다시 fully connected layer를 거쳐 다른 node로 전달되는 경우를 살펴보자.

그때 fully connected layer의 weight에 대한 미분은 input값이 된다. 

(출력을 y라고 할 때, $ \frac{\partial y}{\partial w_i} = x_i $)

이때의 input은 sigmoid의 출력이므로 모두 양수이고, $ \frac{\partial L}{\partial w_i}$는 역전파를 통해 전달되는 값이 양수라면 모두 양수, 전달된 값이 음수라면 모두 음수가 된다. 

이럴 경우 학습은 매우 비효율적으로 이뤄진다.

예를 들어 w1 = 0.5, w2 = 0.5 이고, 각각 0.4, 0.6일때 최적값이라고 가정해보자.

만약 미분값이 모두 양수이거나 음수가 아니라면 w1 -= 0.1, w2 += 0.1 과 같이 한번만에 최적값에 도달할 수 있을 것이다.

그러나 모두 양수이거나 음수라면 w1 += 0.1, w2 += 0.2 / w1 -= 0.2, w2 -= 0.1 과 같은 순서로 2번 수행되어야 최적값에 도달할 수 있을 것이다. 

즉, sigmoids의 출력이 zero-centered가 아니라서 학습(weight의 최적화)이 비효율적으로 이뤄지게 된다.

(3) exp() is a bit compute expensive

말 그대로 exp()의 연산 자체가 조금은 부담스럽다는 문제도 존재한다.

(1), (2)번에 비해서는 사소한 문제이다.

zero-centered하지 않은 문제를 극복한 tanh(x)도 존재하지만 마찬가지로 수렴하는 부분에서 미분값이 0에 수렴한다. 

● ReLU

ReLU 함수는 sigmoid의 문제를 극복하여 가장 많이 사용되는 activation 함수이다.

다음과 같은 장점이 있다. 

(1) 미분값이 0으로 수렴하지 않는다. (+ 영역에서)

(2) max(0, x)로 구현할 수 있어 계산이 가볍다.

(3) simgoid나 tanh보다 학습이 더 빨리 이뤄진다.

(4) 실제 생물학적 activation과 가장 유사하다.

그러나 ReLU에도 단점은 존재한다.

(1) 여전히 zero-centered 되어있지 않다.

(2) Dead ReLU problem

Dead ReLU란 어떤 training data에 대해서도 0을 출력하는 ReLU를 의미한다.

(any input이라는 표현이 많아서 헷갈렸는데, any training data가 맞다.

input을 억지로라도 조정하면 당연히 active하게 만들 수 있을 것이다.)

Dead ReLU가 발생하면 미분값도 0이 되고, 업데이트도 이뤄지지 않는 문제가 발생하다. 

말그대로 기능을 못하는 dead ReLU가 되는 것이다.

Dead ReLU는 크게 2가지 이유로 발생한다.

 1. wrong initialization

 weight의 초기화 자체가 잘못된 경우, 간단하게 예를 들어 weight가 모두 음수로 초기화 되면 ReLU의 output은 항상 0   일 것이다. (이전의 input은 모두 양수 가정)

 -> 초기화 시에 slightly postivie biases를 주기도 한다고 한다. 

 2. Too big learning rate

 Learning rate가 너무 큰 경우에도 학습이 잘못이뤄져 dead ReLU를 발생하기 쉽다고 한다. 

이에 대한 명확한 해결은 강의 시점에서 존재하지 않는다고 하고, 보통 10~20% 정도의 dead ReLU가 발생하지만 학습에 지장을 갈 정도로 문제가 되진 않는다고 한다.

Leaky ReLU나 ELU를 사용해서 dead ReLU를 방지하는 방법도 있다. 

실제로는 위의 룰을 따르는 것이 일반적이라고 하다.

- Data Preprocessing

일반적으로 이미지 데이터를 다루기 위해서는 zero-centered data로 만드는 것 외에 별도의 전처리는 크게 필요하지 않다. (zero-centered가 필요한 이유는 이전 activation function에서 다룬 내용과 동일하다. 학습이 비효율적으로 이뤄지기 때문)

Scaling이 필요한 이유도 각 feature가 비슷한 scale을 갖게 하기 위해서인데, image data의 경우 이미 각 pixel의 scale이 통일되어 있다.

- Weight Initialization

Weight의 initialization 또한 중요하며 고려할 점이 몇가지 있다.

● 전부 0으로 초기화

가장 먼저 모든 weight를 0으로 초기화하는 경우를 생각해보자. 

모든 layer, 모든 노드가 같은 출력을 할 것이고 가중치 업데이트도 동일하게 이뤄질 것이다. 

즉, 노드를 여러개 만드는 의미가 없어진다. 

이런 문제에 대해 Symmetry breaking이 필요하다고 한다.

● Gaussian with mean = 0, std = 1e-2 or 1

Symmetry breaking을 하면서, 적당한 random 값으로 초기화하자는 발상이다.

결론적으로 말하자면 층이 깊어질수록 잘 동작하지 않는다. 

각 layer마다 500개의 neurons가 존재하는 10-layer net에 대해 해당 초기화를 실험한 결과는 다음과 같다.

(activation function은 tanh를 이용했다고 한다.)

각 layer마다 각 neuron의 출력결과를 시각화한 결과이다. 

0-mean Gaussian으로 초기화했으므로 mean이 0인 것은 문제되지 않지만, 점점 표준편차도 0에 수렴하는 것을 확인할 수 있다(모든 neuron이 거의 0을 출력). 

tanh의 범위는 [-1, 1]이고, 계속해서 mean = 0, std = 1-e2로 초기화하였으므로 대부분 0과 가까운 작은 값이 곱해질 것이다.

그 결과 층이 깊어질수록 모든 뉴런이 거의 0을 출력하게 될 것이다.

-> 마지막 layer에서는 미분값이 거의 0일 것이고, 역전파를 통해 전달되는 값도 사라지기 때문에(local 미분 = input 값) 학습이 이뤄지지 않는다. 

이번엔 std를 1로 초기화한 실험이다.

1보다 큰 값이 곱해져서 더해진 후 tanh를 통과하기 때문에 대부분의 경우에서 -1이나 1에 가까운 출력을 보이게된다. 

따라서 모든 미분값이 거의 0에 수렴할 것이고, 학습이 이뤄지지 않는다. 

● Xavier initialization

std를 $ \frac{1}{\sqrt{n}} $로 초기화하는 방법이다. (n : 각 layer별 input size)

가장 좋은 초기화 방법으로, 각 layer별 출력이 정규분포를 근사적으로 따르는 모습을 확인할 수 있다.

이러한 설정에 대한 이론적 배경은 논문에 자세히 나와있다고 한다. 

그러나 ReLU에 대해서 Xavier 초기화를 사용하면 또 다시 위와 같은 문제가 발생한다. layer를 거칠수록 양수의 절반은 0이 되므로, 나중에는 대부분의 출력이 0이 된다. 

따라서 ReLU에 대해서는 std를 $ \frac{1}{\sqrt{n/2}} $로 초기화한다.

Input 중 절반은 inactive되어 오므로 input을 절반으로 생각하는 Xavier 초기화와 유사하게 생각하면 된다. 

이럴 경우 절반은 양수, 나머지는 inactive되는 결과가 모든 layer에서 유지된다.

(절반은 0이 되는 것이 자연스러운 출력이다.)

- Batch Normarlization

앞서 layer들의 출력을 안정화하기 위해 activiation 함수를 변경하고, 다양한 weight 초기화에 대해 살펴보았다.

2015년에 제시된 batch normarlization은 안정화를 위해 제시된 또 다른 방식이다.

아이디어는 다음과 같다.

“you want unit gaussian activations? just make them so.”

Gaussian 분포를 따르기 원한다면 그렇게 만들면 된다는 아이디어이다.

Batch noralization을 수행하는 하나의 layer가 추가된다고 생각하면 된다.

보통 Fully connected layer와 activation function 사이에 추가한다고 한다.

그러나 생각해보면, 반드시 평균이 0이고 표준편차가 1인 표준정규분포가 될 필요는 없다.

따라서 각 batch 별로 normalization을 수행한 후, $ \gamma$를 곱해주고(표준편차 변형), $\beta$를 더해주는(평균 변형) 과정을 통해 약간의 변형을 더한다.

여기서 $ \gamma, \beta$ 또한 학습되는 parameter로, 성능을 좋게 만드는 더 좋은 분포가 있다면 그렇게 바꾼다는 원리로 이해할 수 있다. 

최종적으로 위와 같이 정리할 수 있다.

전체적으로 학습을 안정화시키며(imporves gradient flow, allow higher learning rate),

앞서 다룬 initialization 문제의 의존도를 낮춘다고 한다.

또한 일종의 regularization 역할도 하게 되는데, batch마다 empirical mean이 다르기 때문에 같은 input이라도 출력이 deterministic하지 않기 때문이다. 

- Babysitting the learning process

모델을 학습시키는 과정은 보통 다음과 같은 process를 따른다.

Step1. Data Preprocessing

대부분의 이미지 데이터의 경우 zero-centered data로 만들어주면 된다.

Step2. Choose the architecture

모델의 구조를 선택하는 과정이다. 

가장 좋은 구조를 찾기 위해서는 다양한 시도를 해봐야하지만, 기본적으로 다음 과정을 따르면 좋다.

먼저 설계상 문제는 없는지 다음 두 가지 사항을 검사한다.

 - Random initialization했을 경우 loss는 예상대로 나오는지, ('log Class의 수'정도가 나와야된다.)

 - 적은 sample data에 대해서는 100% overfit이 가능한지 

다음으로 regularization 을 조금 추가하고, 학습에 적절한 learning rate를 찾는다.

 learning rate가 너무 작으면 loss가 거의 낮아지지 않을 것이ㅗㄱ,

 반대로 너무 크면 loss가 exploding할 것이다.

- Hyperparameter Optimization

Validation set을 이용하여 optimization을 수행한다. 

Assignment1에서 grid layout 방식을 주로 사용했지만, random layout이 최적 parameter를 찾을 확률이 더 크다고 한다. 

그림에 나와있듯이, 특정 parameter가 더 영향을 크게 미친다고 했을 때,grid 방식에서는 3가지 값을 시도해보지만 random 방식에서는 9가지 방식을 시도하게 된다. 

학습 과정을 시각화하고 확인하여 문제를 찾을 수도 있다.

예를 들어 위와 같이 taining accuracy와 validation accuracy가 크게 차이나면 overfitting 문제가 발생하고 있음을 확인할 수 있고, regularization parameter를 수정하는 등의 보완을 할 수 있을 것이다. 

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Lecture5에서는 Convolutional Neural Network이 무엇이고, 어떻게 동작하는지에 대해 설명하고 있다.

- History

먼저 CNN의 역사에 대해 설명하고 있다.

다양한 이미지를 보여주면서 고양이의 뇌파를 추적해본 유명한 실험이다. 

각각의 모양, 특징마다 반응하는 영역이 달랐다. 

이후 초기의 CNN구조에 대한 연구에서도 층을 hierical하게 쌓고, sandwich 구조를 통해 

간단한 특징과 복잡한 특징에 대해 구분되어 반응할 수 있도록 설계하게 된다. 

이어서 AlexNet과 같은 최근의 구조를 설명하고,

다양한 쓰임(classification, 동작 인식, segmentation 등)에 대해 간단하게 소개하고 있다. 

- 구조

● Convolution Layer

먼저 기존의 Nueral Network에서 다뤘던 layer인 fully connect layer는 input을 하나의 vector로 전환하고, weight vector와 곱하여 output을 출력한다.

이와 다른 Convlution Layer의 가장 큰 특징은 input의 spatial structure를 유지한다는 것이다.

기본적으로 Filter가 input image의 각 영역을 slide하며 연산을 수행하게 된다.

위 이미지는 32x32x3 크기의 이미지의 하나의 영역과 5x5x3 filter의 연산을 나타내는 이미지로, 각 영역마다 하나의 값을 출력하게 된다. 

연산 내용을 벡터로 나타내고 있는데, elementwise 곱의 sum과 동일하다. 

(※ 사실 기존에 convolution 연산에서 필터와 각 영역의 elementwise곱을 하는 것이 어떤 의미인지 정확히 감이 안왔었는데, 내적으로 이해하면 filter가 특정 영역에 반응한다는 것이 어떤 의미인지 더 와닿았다.)

stirde = 1 이라고하면 출력은 28x28x1 이 될 것이고, 또 다른 필터를 적용하면 새로운 28x28x1 output이 출력될 것이다. 

(stride : filter가 이동하는 보폭)

※ 수업 질문 :

Q) stride 설정 시 고려할 점은 무엇인지?

A)

downsampling : pooling과 같은 효과를 stride를 통해서도 얻을 수 있음.

# of parameters : 전체 모델의 parameters 수를 줄일 수 있음. 

                       그러나 stride를 늘려 parameter를 줄이는 것은 information loss이므로, 성능에는 안 좋을 수 있음.

(모델 크기-복잡도 trade-off)

ConvNet은 기본적으로 위와 같은 구조를 갖게 된다. 

앞서 간단한 특징부터 복잡한 특징까지 서로 다른 영역이 반응한다고 했는데, CNN 역시 그런 특징을 보인다.

VGG-16(CNN 모델)의 학습된 Weight를 시각화한 결과이다.

앞의 layer의 weight일수록 '선'과 같이 비교적 low-level feature를 보이고, 깊어질수록 high-level feature를 보인다. 

Pooling에 대해서는 아직 다루지 않았지만, 결국 CNN의 원리를 다음과 같이 정리할 수 있다.

(1) 각 filter별로 학습된 weight는 feature에 대한 정보이다. 즉, 각 filter별로 어떠한 특징에 반응한다.

('Deep learning에서는 feature를 스스로 학습한다'는 의미가 더욱 와닿는다.)

Convolution 연산을 거치며 주어진 image에서 해당 feature 관련 정보를 추출한다.

(2) 깊은 layer의 filter일수록 복잡한 feature 정보를 추출한다.

(3) 마지막 layer에서 각 feature 정보를 종합한 새로운 feature(사람이 이해하기 어려운)가 출력될 것이고, 해당 feature를 통해 fully connect layer를 거쳐 classification을 진행한다. 

● Padding

stride = 3, 7x7 크기의 이미지라면 3x3 크기의 필터를 적용할 수 없을 것이다. 

따라서 상하좌우로 0을 채워 이미지 크기를 조정할 때, zero padding을 사용한다.

7x7 크기의 이미지에 pad = 1을 적용한 후, 3x3 filter를 거치면 output은 input의 shape와 동일한 7x7 이미지가 된다.

이처럼 output 크기를 조정하기 위해서도 padding은 사용된다. 

Input의 크기, filter의 크기, padding 정보 그리고 stride 값이 주어질 때, output의 크기는 위와 같이 공식화 할 수 있다.

● Pooling layer

Pooling layer는 학습되는 layer는 아니다.

연산을 통해 image를 downsampling하는 등의 역할을 수행한다.

대표적으로 max poling 연산이 있다.

※ 수업 중 나온 질문 :

Q) Average pooling보다 max pooling이 선호되는 이유?

A) Average pooling도 사용할 수 있다. 다만 max pooling을 사용하면 어떤 특징에 response하는지 안하는지에 대해서 좀 더 집중할 수 있을 것이다. 

● Fully Connected Layer

앞서 정리한 것처럼, convolution layers를 거치며 추출된 정보를 input하는 일반적인 nueral network처럼 동작한다. 

※ 수업 질문 :

Q) 그럼 언제쯤(얼마나 많은 convolution layer를 지나고) fully connected layer를 삽입해야되는지?

A) 실험적으로 결정해야 된다.

각 layer의 의미를 고려하면서 여러 실험을 진행하면 좋다.

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Assignment1의 마지막 과제인 Q5에서는 이미지로부터 feature를 extraction한 후 extraction한 feature에 대해 학습하는 내용을 다루고 있다.

feature extraction 코드로 제공되고, 앞선 과제에서 만들어둔 model을 이용하여 실험을 진행한다.

Lecture3의 슬라이드로, feature eatraction을 거친 후 training하는 것과 raw pixel을 통해 training하는 과정의 차이를 보여준다.

- 0. Extract Feature

우선 앞선 과제들과 동일하게 CIFAR10 데이터를 사용하고, 제공되는 feature extraction 코드를 이용해 새로운 data로 생성한다.

ex) X_train -> X_train_feats

참고로 Histogram of Oriented Gradients(HDG) 와 color histogram에 대한 feature를 추출한다고 한다.

- 1. Train Linear SVM

먼저 Linear SVM 모델에 대해 학습을 진행해본다.

learing_rate 등의 파라미터를 조정하여 40% 이상의 정확도가 나와야 된다고 한다.

실험에 대한 코드는 생략하고,

learning rate와 regularization strength 그리고 num_iters를 적절히 조정하여 조정하여 47%의 정확도를 얻을 수 있었다.

Q2에서 SVM을 통한 정확도가 40% 정도로 나왔던 것을 생각해보면, 단순 raw pixel을 이용한 것보다 더 좋은 성능을 보이는 것을 확인할 수 있다.

- train 2-layer network

다음으로는 2-layer network에 대해 실험을 진행한다. 

여태까지 실험한 모델들 중 가장 좋은 성능을 보일 것이라고 한다.

(55%~60%의 정확도)

이미 dropout을 추가로 구현해놨기 때문에, learning_rate와 num_epochs 만 간단하게 조정하면서 실험을 진행한 결과, 

59%의 정확도를 달성할 수 있었다.

2 layer net만으로도 60% 정도의 정확도를 달성할 수 있을 정도로, feature extraction을 통해 큰 성능 향상을 얻을 수 있었다.

※ 본 내용은 stanford에서 제공하는 cs231n 강의, 강의자료를 바탕으로 작성하였습니다.

Q4에서는 affine 계층 및 SVM, softmax loss를 layer로 구현한 후, layer들을 이어붙여 2-layer Neural Network를 구현하는 내용을 다룬다. 

- Setup

이전 과제들과 마찬가지로 CIFAR10 data를 load하여 사용하고, shape는 위와 같다. 

- Affine Layer (Forward/Backward)

● Forward

Affine layer의 forward 연산은 굉장히 단순하므로 코드는 생략하겠다. 

N : 데이터의 수, D : 데이터의 차원, M : class의 수라고 할 때,

X = NxD, W = DxM 으로, X와 W의 곱만 수행하면 된다(+bias). 그 결과는 NxM 크기의 행렬이 된다. 

● Backward

역전파의 경우도 사실 계산은 간단하기 때문에 코드는 생략하겠다.

X, W, b에 관한 미분을 각각 dX, dW, db 라고 하면 

위와 같이 계산된다.

사실 affine 계층의 역전파 수식은 자주 쓰여서 알고 있었고, 또 shape를 맞추면 된다는 설명을 통해서 쉽게 기억할 수 있었다.

그러나 행렬과 행렬의 미분을 유도하는 과정은 쉽지 않았다.

(0) 행렬과 행렬의 미분?

가장 문제가 된 부분은 위와 같은 미분이다. 

막상 유도를 하려다 보니 행렬과 행렬의 미분 자체에 대한 정의가 애매했다.

구글링을 해봐도 행렬과 행렬의 미분에 대한 정의가 명확하게 나온 자료가 없었고, 사실 수학적으로 명확한 정의가 없다는 내용도 있었다.

matrix-scalar 미분 -> matrix-vector 미분 -> matrix-matrix 미분 의 순서로 확장하면 미분을 정의할 수 있다고 한다. 

그러나 계산 그래프를 이용하는 대부분의 경우에는 아래와 같이 행렬과 행렬의 미분을 적용하지 않고도 바로 역전파를 계산할 수 있다.

(1) L이 scalar인 경우

http://cs231n.stanford.edu/handouts/linear-backprop.pdf)의 자료를 바탕으로 이해했다. 

(※ 이 부분에 대한 설명은 위 링크의 자료를 이용하였습니다.)

$\frac{\partial Y}{\partial W} $를 직접 계산하기 보단, chain룰을 이용한다. 

간단하게 X와 W가 위와 같다고 하자.

$ \frac{\partial L}{\partial Y}$는 스칼라를 행렬로 미분하는 방법을 통해 얻을 수 있다. 

스칼라를 행렬로 미분하는 방법을 몰랐더라도, 위 식을 보면 이해할 수 있을 것이다. 

마찬가지로 $ \frac{\partial L}{\partial X}$도 식 (6)과 같이 나타낼 수 있고, $ x_{1, 1}$의 식에 집중하면 식 (7)과 같이 나타낼 수 있다.

(2개의 시그마가 붙는 이유에 대해서는 편미분을 확인하면 된다.)

다시 (7)의 식을 좀 더 직관적으로 표시해보면, 

(10) -> (11)로 가는 과정이 이상하게 보일 수 있는데, 식 (7)의 시그마를 간단히 표현하기 위해 나타낸 것이라고 생각하면 된다. 

다른 경우에 대해서도 일반화해보면 $ \frac{\partial L}{\partial Y}$ 의 식은 유도할 수 있다.

- ReLU (forward/backward)

● Forward

마찬가지로 ReLU도 forward는 매우 간단하므로, 구현은 생략하겠다.

● Backward

Backward는 직관적으로 구현하긴 했지만,

활성화되는 경우는 그대로 전달되므로 미분값이 1, 그렇지 않으면 0으로 구현했다.

결국 정답은 맞았지만 이 부분도 행렬과 행렬의 미분이라 조금 더 생각해봐야한다.

- 기타 layers

추가로 softmax와 svm loss를 layer로 구현했다.

해당 부분은 Q2, Q3에서 다룬 내용과 거의 동일하므로 생략하겠다.

- 2-Layer Net

다음으로 앞서 구현한 layer들을 이용하여 2-layer network를 구현했다. 

먼저 구현 내용을 계산 그래프로 구현하면 위와 같다.

코드로 구현한 내용은 위와 같다.

'dropout 계층 추가 실험' 주석 밑의 if문을 제외하면 앞서 계산그래프와 동일하다.

~_forward 연산은 앞서 구현했고 코드를 생략한 내용이지만 직관적으로 이해할 수 있을 것이다.

다만 반환값의 경우 (forward 연산값, input) 값이다. 역전파 계산시 필요한 값을 forward에서 return하고 cache_~ 로 저장하여 관리한다.

※ 수정 : Dropout의 출력이 잘못되어있다. Dropout을 적용할 시, test time에는 dropout확률을 곱해줘야한다. 

● dropout

dropout은 뒷부분에서 튜닝을 통해 성능을 올리는 과제를 진행하는 과정에서 추가한 것인데, 코드가 나왔으므로 같이 살펴 보겠다.

먼저 계산 그래프로는 다음과 같다.

dropout 역시 하나의 layer로 생각하면 된다.

dropout에 대해서는 다음 그림이 잘 설명하고 있다.

학습 시에 random하게 일부 class에 대한(hidden layer일 경우라도 class라고 표현했다.) score를 비활성화하여(0으로 만들어서 없는 것처럼 동작) 줄여 과적합을 방지하는 기법이다.

코드를 보면 dropout이 True인 경우 random하게 선택된 class의 score를 0으로 만든다는 것을 확인할 수 있다.

다음으로 loss를 계산하고 미분값도 return하는 코드이다. 

loss를 계산하면서 동시에 미분을 계산하는 방식으로 구현되어 있다.

미분은 각 layer마다 backward로 구현해두어서, 역전파 순서대로만 진행을 하면 된다.

dropout의 경우 drop한 class의 열에만 0을 곱해주면 된다.

(ReLU의 경우와 비슷하다.)

추가로 앞서 설명에 regularization term이 빠져있는데, 그 부분만 추가해주면 2-layer network가 완성된다. 

(regularization term은 미분의 편리함을 위해 0.5를 곱해준다)

- train

다음으로 Solver class를 이용해서 train을 진행하는 내용이다.

Solver의 경우 train을 진행해주는 class로 model(앞서 구현한 2-layer network)과 데이터 그리고 기타 설정을 인자로 전달해주면 model을 학습시켜주는 class라고 이해하면 된다.

제공된 코드로 꽤 복잡하지만 우선 핵심적으로 다음 흐름만 이해하면 될 것 같다.

 - init을 통해 여러 설정 초기화(learning rate, batch size 등등)

 - train이 시작되면 매 iteration마다 step 호출

 - step에서는 SGD를 활용하여 weight update

사용 자체는 매우 간단하다.

제공된 설명에 따르면 default 세팅으로 처음 train을 돌리면 대략 36% 정도의 validation 정확도가 나와야된다고 하는데, 기본설정에서도 40% 이상의 정확도가 나오긴했다.

(첫번째 실험 시에는 dropout을 추가하지 않았음.)

시각화 코드도 제공해서, 꽤 높은 퀄리티로 training process를 경험해볼 수 있다. 

● Tuning

마지막으로 튜닝을 통해서 validation 성능을 48%이상으로 높이고 test 성능도 48% 이상 나오게 하라는 과제가 있었다.

다양한 수정을 해도 상관이 없다고 한다(ex) dropout).

최종 코드는 위와 같지만, 실험은 다음과 같이 진행했다.

  1. learning_rate와 reg(regularization strength)와 num_epochs의 여러 조합에 대해 비교

  2. 그 중 가장 좋은 model을 찾았지만 validation accuracy가 48%를 넘지 못했음.

  3. 시각화 결과 과적합 문제가 있어서, dropout도 추가(2-Layer Net에 추가로 구현한 부분)

 (Solver._step()에서 loss를 계산할 때(미분을 계산할 때) dropout 옵션을 True로만 설정하면 된다.)

그 결과 validation과 test에 대해 각각 50%와 49%의 정확도를 달성할 수 있었다.

최대 score가 52% 라고 한다.